|
|
|
| All Solutions of Type: Mechanics | | 0 | Click here to jump to the problem! | GR8677 #1
|
Mechanics }Newtonian }Newtonian
This problem can be translated into an equation:

Note that the sign is compensated for. 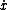 is positive going up (so that is positive going up (so that  acts in the same direction as gravity), and it is negative going down (acting in the opposite direction of gravity). acts in the same direction as gravity), and it is negative going down (acting in the opposite direction of gravity).
\par
(A)  because because )
(B) True. 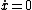 at the top. Thus, plug that into the equation in described in (A) and get at the top. Thus, plug that into the equation in described in (A) and get 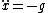
(C) ) could be greater than could be greater than 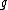 , especially when , especially when 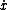 is positive in sign. is positive in sign.
(D) The wind friction ( ) term would change sign when going downwards. (See the Note above.) Thus, the equation of motion presented above would be different in sign going down and up. (Also, one could argue that after the force of wind friction acts, to conserve energy, kinetic energy must lessen in the final energy sum. Thus, the final velocity can't be the same as ) term would change sign when going downwards. (See the Note above.) Thus, the equation of motion presented above would be different in sign going down and up. (Also, one could argue that after the force of wind friction acts, to conserve energy, kinetic energy must lessen in the final energy sum. Thus, the final velocity can't be the same as 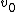 . Or, intuitively, one could see friction as a symmetry breaker, viz., the ideal parabolic path is disturbed in such a way that the end velocity changed.) . Or, intuitively, one could see friction as a symmetry breaker, viz., the ideal parabolic path is disturbed in such a way that the end velocity changed.)
(E) Since the force other than gravity is a frictional force, which, by definition, slows down the object, the final velocity has to be less than 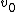 . .
|
| 1 | Click here to jump to the problem! | GR8677 #2
|
Mechanics }Vector }Vector
While there may be a more quantitative solution, the simplest solution is qualitative, based on elementary vector addition and knowledge of the force center.
The problem states that the object orbits the Earth in a perfect circle, initially. This means that the initial velocity (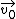 ) is perpendicular to the vector pointing to the earth center ( ) is perpendicular to the vector pointing to the earth center (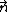 ), i.e., it's tangent to the circular path. This is the condition for uniform circular motion (the centripetal acceleration is due to the Gravitational Law). ), i.e., it's tangent to the circular path. This is the condition for uniform circular motion (the centripetal acceleration is due to the Gravitational Law).
After firing a missile straight to Earth center, its velocity gains an extra normal component ( ), equal and opposite to the velocity of the missile fired to Earth. Thus, its trajectory would deviate from the circular trajectory. ), equal and opposite to the velocity of the missile fired to Earth. Thus, its trajectory would deviate from the circular trajectory.
Because the only source of acceleration comes from the Earth center,  , which is parallel to the centripetal acceleration provided by the Earth, will eventually go to 0. Recall that acceleration does not effect velocity components in the perpendicular direction (to wit: a projectile fired on Earth has the same constant , which is parallel to the centripetal acceleration provided by the Earth, will eventually go to 0. Recall that acceleration does not effect velocity components in the perpendicular direction (to wit: a projectile fired on Earth has the same constant  , but its , but its 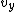 changes). There will thus always be a (nearly constant) tangential velocity, even at the perigees. However, changes). There will thus always be a (nearly constant) tangential velocity, even at the perigees. However,  will go to 0 at the perigees. The tangential velocity will remain more-or-less constant, so that instead of spiraling inwards, the path becomes an ellipse, as will go to 0 at the perigees. The tangential velocity will remain more-or-less constant, so that instead of spiraling inwards, the path becomes an ellipse, as  is restored at the apogees and zero'ed at the perigees. is restored at the apogees and zero'ed at the perigees.
(In a more down-to-earth form, this problem is essentially a projectile firing question with no numerical work involved.)
|
| 3 | Click here to jump to the problem! | GR8677 #6
|
Mechanics }Vectors }Vectors
Since there is only one force acting, i.e., the gravitational force, one can find the tangential acceleration by projecting  in the tangential direction. Equivalently, one dots gravity with the tangential unit vector, in the tangential direction. Equivalently, one dots gravity with the tangential unit vector, 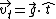 . .
There's a long way to do this, wherein one writes out the full Gibbsean vector formalism, and then there's a short and elegant way. (The elegant solution is due to Teodora Popa.)
The problem gives 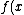 = y = x^2/4) . Thus, . Thus, 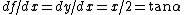 , where in the last step, one notes that the ratio , where in the last step, one notes that the ratio  forms the tangent of the indicated angle. forms the tangent of the indicated angle.
One recalls the Pythagorean identity 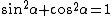 , and the definition of , and the definition of 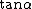 in terms of in terms of 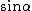 and and 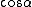 . Thus, one gets . Thus, one gets 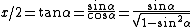 . Square both sides to get . Square both sides to get 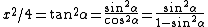 . .
Solve 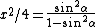 to get to get 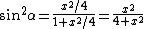 . .
The angle between the vectors  and and 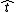 is is 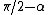 , and thus the tangential acceleration is , and thus the tangential acceleration is 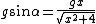 . .
Beautiful problem.
|
| 4 | Click here to jump to the problem! | GR8677 #7
|
Mechanics }Statics }Statics
Straight-forward Newtonian statics:
\Rightarrow T\sin(\theta)=F<br />
)
-mg\Rightarrow T\cos(\theta)=mg<br />
)
Divide the two equations above, cancel T's, and get: \par
=\frac{F}{mg}=\frac{10}{2*10}=.5) . Choice A is right. . Choice A is right.
|
| 9 | Click here to jump to the problem! | GR8677 #37
|
Mechanics }Statics }Statics
Sum over each component. Note that the horizontal direction has a net force proportional to the centripetal acceleration 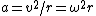 , where , where 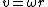 . Note that . Note that  is the tension. is the tension.
&=&mv^2/r=m\omega^2r\\
\sum F_y=T \cos(\theta/2)-mg&=&0=<br />
\end{eqnarray})
Solve for T above to get,
&=&m\omega^2r\\
\sum T \cos(\theta/2)&=&mg<br />
\end{eqnarray})
Find the magnitude of T and use the Pythagorean theorem,
+T^2 \sin^2(\theta/2)}=m\left(g^2 + \omega^4 r^2 \right)^{1/2},<br />
)
and thus (E) is the right answer.
(The above should be fairly obvious, but if one is totally clueless, then one can eliminate choice (D) from noting units. The angular velocity has units of 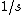 but but 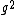 has time units proportional to has time units proportional to 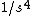 .) .)
|
| 11 | Click here to jump to the problem! | GR8677 #43
|
Mechanics }Normal Modes }Normal Modes
Because there are two degrees of freedom in this problem, there are two normal mode frequencies.
Because there is no external torque acting on the system, the center of mass of the system stays the same through time.
From common sense, one deduces that 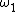 has to do with the outer masses moving perfectly out of phase, i.e., masses A and C moving either towards the left and right (away from each other), respectively, or right and left (towards each other), respectively---and B being perfectly stationary, thereby ``conserving" the center of mass. has to do with the outer masses moving perfectly out of phase, i.e., masses A and C moving either towards the left and right (away from each other), respectively, or right and left (towards each other), respectively---and B being perfectly stationary, thereby ``conserving" the center of mass.
The other angular frequency,  , has to do with either masses A and C moving in phase and mass B out of phase. , has to do with either masses A and C moving in phase and mass B out of phase.
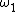 is actually equivalent to having a single mass on a string, since because the middle mass doesn't move, it acts as a sort of support for the spring. is actually equivalent to having a single mass on a string, since because the middle mass doesn't move, it acts as a sort of support for the spring. 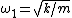 , which would correspond to choice (B). (Of course, one should recall the obvious, that , which would correspond to choice (B). (Of course, one should recall the obvious, that 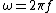 .) .)
(Incidentally, one can derive  without having to resort to the formalism of matrix mechanics: Since the center of mass remains 0, one has without having to resort to the formalism of matrix mechanics: Since the center of mass remains 0, one has 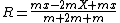 . Solving, one gets . Solving, one gets 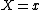 . The displacement of the middle mass, mass B, is thus . The displacement of the middle mass, mass B, is thus 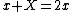 , while the displacements of the smaller masses, masses A and C, are both , while the displacements of the smaller masses, masses A and C, are both  . The displacement of each spring is . The displacement of each spring is 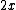 . Potential energy is thus . Potential energy is thus ^2=\frac{1}{2}8kx^2) . The kinetic energy is . The kinetic energy is ^2+\frac{1}{2}(2m)(\dot{x})^2=\frac{1}{2}4m(\dot{x})^2) . The normal mode frequency is deduced by . The normal mode frequency is deduced by 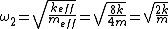 ) )
|
| 12 | Click here to jump to the problem! | GR8677 #44
|
Mechanics }Conservation of Momentum }Conservation of Momentum
One could use energy, but then one would have to take into account the inertia. Momentum might be easier,
 = (p_f=MV)\Rightarrow V=\frac{m}{M}v,<br />
)
where the final momentum takes into account the fact that the final velocity of the particle is at rest (0). And, so it is (A)!
|
| 18 | Click here to jump to the problem! | GR8677 #78
|
Mechanics }Conservation of energy }Conservation of energy
There isn't much to say about this problem other than the fact that it's a conceptual conservation of energy problem. Particle 1 moves at velocity  towards particle 2, initially at rest. EM-potential energy increases as they get closer and closer together---but, energy should still be conserved since no energy is radiated. The potential energy increase comes from the initial kinetic energy of particle 1. Take choice (C). (The other choices are all either too weird or just plain bogus.) towards particle 2, initially at rest. EM-potential energy increases as they get closer and closer together---but, energy should still be conserved since no energy is radiated. The potential energy increase comes from the initial kinetic energy of particle 1. Take choice (C). (The other choices are all either too weird or just plain bogus.)
|
| 19 | Click here to jump to the problem! | GR8677 #93
|
Mechanics }Power }Power
Recall the following basic formulas, 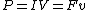 , where , where 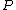 is power, is power, 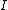 is current, is current, 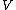 is voltage, is voltage, 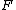 is force, and is force, and  is velocity. is velocity. 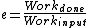 , where , where  is the efficiency, which relates work (and thus power). is the efficiency, which relates work (and thus power).
The problem gives 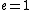 , ,  , , 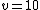 , , 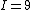 , , 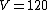 ---where all units are SI. ---where all units are SI.
Thus  . Solve for . Solve for 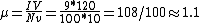 , as in choice (D). , as in choice (D).
|
| 23 | Click here to jump to the problem! | GR8677 #7
|
Mechanics }Elastic Collisions }Elastic Collisions
One determines the velocity of impact of the ball from conservation of energy,
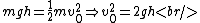
Conservation of momentum gives,
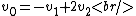
Conservation of kinetic energy gives,
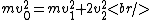
Plug in the momentum and kinetic energy conservation equations to solve for 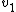 and and 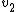 in terms of in terms of 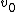 to get to get
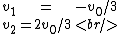
Write yet another conservation of energy equation for the final energy,
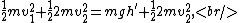
where the condition that the mass 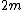 slides on a frictionless plane is used. slides on a frictionless plane is used.
Thus, 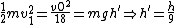 , where the previous result , where the previous result 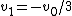 and and 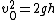 is used. is used.
|
| 24 | Click here to jump to the problem! | GR8677 #8
|
Mechanics }Damped Oscillations }Damped Oscillations
One should remember that damped oscillations have decreasing amplitude according to an exponential envelope. As the amplitude shrinks, the period increases. The additional force instated in the problem is equivalent to damping, and thus the period increases, as in choice (A).
|
| 26 | Click here to jump to the problem! | GR8677 #21
|
Mechanics }Moment of Inertia }Moment of Inertia
To solve this problem, one should remember the parallel axis equation to calculate the moment of inertia about one end of the hoop:
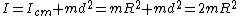 , ,
where  is the distance from the pivot point to the center of mass, which in this problem, is just equal to is the distance from the pivot point to the center of mass, which in this problem, is just equal to 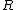 . (In the last equality, note that the moment of inertia of a hoop of radius R and mass m about its center of mass is just . (In the last equality, note that the moment of inertia of a hoop of radius R and mass m about its center of mass is just 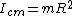 .) .)
The problem gives the period of a physical pendulum as 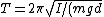}) . Thus, plugging in the above result for the moment of inertia, one has, . Thus, plugging in the above result for the moment of inertia, one has, 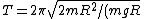}=2\pi \sqrt{2R/(g)} \approx 2*3\sqrt{2*0.2/(10)}= 12/10=1.2s) , which is closest to choice (C). (Since , which is closest to choice (C). (Since  was rounded to 3, the period should be slightly longer than 1.2s.) was rounded to 3, the period should be slightly longer than 1.2s.)
|
| 28 | Click here to jump to the problem! | GR8677 #23
|
Mechanics }Stability of Orbits }Stability of Orbits
The gravitational force suspect to a bit of perturbation is given as 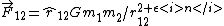 . .
One can narrow down most choices by recalling some basic facts from central force theory:
(A) No mention is made of frictional effects, and thus energy should be conserved.
(B) Angular momentum is always conserved since the net torque is 0 (to wit: the force and moment arm are parallel).
(C) This is just Kepler's Third Law applied to this force. (Recall the following bromide: The square of the period is equal to the cube of the radius---for the inverse square law force. For a perturbed force, the bromide becomes: The square of the period is equal to the 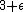 power of the radius.) power of the radius.)
(D) Recall Bertrand's Theorem from Goldstein. Stable non-circular orbits can only occur for the simple harmonic potential and the inverse-square law force. This is of neither form, and thus this choice is FALSE.
(E) Circular orbits exist for basically all potentials. A stationary orbit exists if and only if the following conditions are satisfied:  . Recall that the potential is related to the force by . Recall that the potential is related to the force by 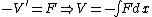 . Use . Use 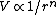 , and recalling the extra term added to the effective potential to be , and recalling the extra term added to the effective potential to be ) , one chunks out the derivatives to get the condition that , one chunks out the derivatives to get the condition that 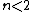 , as a potential exponent, ( , as a potential exponent, (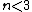 , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For 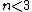 , (the power exponent of the force equation), a stable circular orbit exists. Since , (the power exponent of the force equation), a stable circular orbit exists. Since  is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun. is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun.
|
| 35 | Click here to jump to the problem! | GR8677 #80
|
Mechanics }Wave Phenomena }Wave Phenomena
There's a long way to solve this problem and then a short. One looks at the choices to find the one that first the physical deduction: when 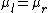 , the whole incident wave should be transmitted, with 0 reflection. Moreover, in the limit of , the whole incident wave should be transmitted, with 0 reflection. Moreover, in the limit of 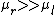 there should be 0 transmission. Choice (C) is the only one that fits this condition, leading to a ratio of 1 for there should be 0 transmission. Choice (C) is the only one that fits this condition, leading to a ratio of 1 for 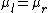 . .
One can also calculate the exact form of the transmission coefficient for this multi-density string. Take the following,
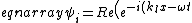} \right)\\
\psi_r = \left( Re R e^{-i(-k_l x-\omega t)} \right)\\
\psi_t = \left( Re T e^{-i(k_r x-\omega t)} \right)<br />
\end{eqnarray})
At the boundary between different density parts, one applies continuity 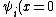+\psi_r(x=0)=\psi_t(x=0)) to get 1+R=T. to get 1+R=T.
One applies 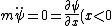 - \frac{\partial \psi}{\partial x}(x>0)) , where , where 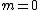 since there is no point particle situated at the origin, to obtain since there is no point particle situated at the origin, to obtain =ik_r T) . .
Recalling the nifty relation 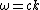 and and  , one solves for T to get , one solves for T to get 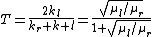 , as in choice (C). , as in choice (C).
|
| 36 | Click here to jump to the problem! | GR8677 #83
|
Mechanics }Rippled Surface }Rippled Surface
The simple intuitive way to solve this is to note that for  , , 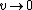 , since one gets an infinitely steep (vertical line) hill, and the only way for the particle to stay on the surface (i.e., not accelerate on it) at the vertical drop is if its velocity is 0. The onyl choice with d on the denominator is choice (D). , since one gets an infinitely steep (vertical line) hill, and the only way for the particle to stay on the surface (i.e., not accelerate on it) at the vertical drop is if its velocity is 0. The onyl choice with d on the denominator is choice (D).
The more rigorous solution is due to Sara Salha.
Equating centripetal force with gravity at the top of the hill, one has 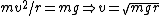 . The non-trivial bit comes from calculating the radius. . The non-trivial bit comes from calculating the radius.
Recall the radius of curvature from calculus 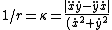^{3/2}}) . Defining a parameter t as the independent variable, and defining . Defining a parameter t as the independent variable, and defining 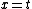 , , 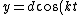) , one finds that , one finds that 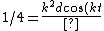}{1+(kd)^2\sin^2(kt)}) . Evaluate it at . Evaluate it at 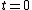 to find to find =k^2d \Rightarrow r=1/(k^2d)) , the radius of curvature at the top of the hill. Plug that into the equation for velocity above to get , the radius of curvature at the top of the hill. Plug that into the equation for velocity above to get  , as in choice (D). , as in choice (D).
|
| 40 | Click here to jump to the problem! | GR8677 #93
|
Mechanics }Potential }Potential
The problem gives a nifty potential energy graph. The period is due to each part of the potential graph.
For the simple harmonic oscillator (SHO) part, one remembers the formula 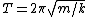 (to wit: (to wit: 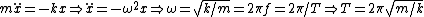 ). However, that period is for a particle to oscillate from one end of the potential curve to the other end and then back again. Since the graph shows only half of the usual SHO potential, the period contribution from the SHO part should be half the usual period: ). However, that period is for a particle to oscillate from one end of the potential curve to the other end and then back again. Since the graph shows only half of the usual SHO potential, the period contribution from the SHO part should be half the usual period: 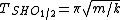
For the gravitational potential, one can calculate the period from the usual kinematics equation for constant acceleration. Recall the baby-physics equation, 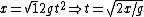 . The quantity needs to be converted to the relevant parameters of the problem. The problem supplies the constraint that the energy is constant, . The quantity needs to be converted to the relevant parameters of the problem. The problem supplies the constraint that the energy is constant, 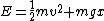 . At the endpoint, one has . At the endpoint, one has 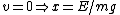 . Plugging this into the equation for time, one gets . Plugging this into the equation for time, one gets 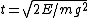 . Since the particle has to travel from the origin to the right endpoint and then back to the origin, the total time contribution from this potential is twice that, . Since the particle has to travel from the origin to the right endpoint and then back to the origin, the total time contribution from this potential is twice that, 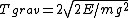 . .
The total period is thus the sum of the above contributions, which is choice (D).
|
| 41 | Click here to jump to the problem! | GR8677 #1
|
Mechanics }Acceleration Vector }Acceleration Vector
This is a conceptual vectors problem.
Tangential: One knows that the velocity of the bob at the endpoints is 0, and that it has maximal acceleration (pulling it back towards the center) at the endpoints. In the center, it has maximal velocity and thus minimal acceleration.
Normal: The normal acceleration varies from 0 at the endpoints to its maximal value at the center. The normal acceleration varies so that the sum of tangential and normal accelerations is a constant.
|
| 43 | Click here to jump to the problem! | GR8677 #3
|
Mechanics }Kepler's Third Law }Kepler's Third Law
Recall Kepler's Third Law stated in its most popular form, The square of the period is proportional to the cube of the orbital radius. (Technically, the orbital radius is the semimajor axis of the ellipse.)
Recast that commonsense fact above into equations to get  , as in choice (D). , as in choice (D).
|
| 53 | Click here to jump to the problem! | GR8677 #56
|
Mechanics }Fluid Statics }Fluid Statics
The physical equation required is the buoyancy equation or Archimedes' Principal. The buoyant force is given by,  . . 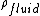 refers to the density of the fluid that buoy's the object. In this case, refers to the density of the fluid that buoy's the object. In this case, 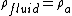 is just the density of air (not Helium). is just the density of air (not Helium).
The buoyant force for this problem is 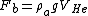 . This force must balance the load carried by the balloon. One now has (approximately, to simplify the calculations, since one is neglecting the weight of Helium) a simple sum of the forces problem, . This force must balance the load carried by the balloon. One now has (approximately, to simplify the calculations, since one is neglecting the weight of Helium) a simple sum of the forces problem, 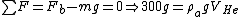 . .
Now, solving for the volume of Helium required, one has 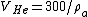 . Since . Since  , this is about , this is about 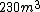 . However, since the balloon has to lift the weight of the Helium as well, the actual volume should be slightly larger. The closest choice is (D). . However, since the balloon has to lift the weight of the Helium as well, the actual volume should be slightly larger. The closest choice is (D).
|
| 54 | Click here to jump to the problem! | GR8677 #57
|
Mechanics }Dimensional Analysis }Dimensional Analysis
The only choice that has the right unit for force is choice (A), since the expression has the units  (m/s)^2 (m^2)=N) . .
|
| 55 | Click here to jump to the problem! | GR8677 #72
|
Mechanics }Forces }Forces
Before the string is cut, one has the basic static equilibrium condition, for each block 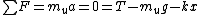 and and 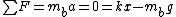 , where , where 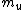 refers to the upper block and refers to the upper block and 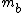 refers to the bottom block. Adding, one has refers to the bottom block. Adding, one has  a = 0 = T-m_ug - m_b) . .
After the string is cut, the tension goes to 0, but one has a non-zero net acceleration. The top mass has  , where the minus sign comes in since the question wants the downward acceleration. The bottom mass has , where the minus sign comes in since the question wants the downward acceleration. The bottom mass has  . But, immediately after the string is cut, the lower mass has 0 acceleration. Thus, . But, immediately after the string is cut, the lower mass has 0 acceleration. Thus, 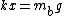 . Plugging this into the equation for the upper mass, one finds that . Plugging this into the equation for the upper mass, one finds that 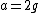 , as in choice (E). , as in choice (E).
|
| 60 | Click here to jump to the problem! | GR8677 #90
|
Mechanics }Normal Modes }Normal Modes
Note that  : :
For figure 1, the potential energy is 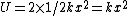 . The kinetic energy is just . The kinetic energy is just 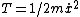 . Thus, . Thus, 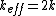 and and 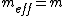 . Thus, . Thus, 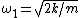 . .
For figure 2, the potential energy is 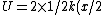^2) , since each spring travels only half as far. The kinetic energy is the same as in figure 1. Thus, , since each spring travels only half as far. The kinetic energy is the same as in figure 1. Thus,  and and 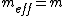 . So, one has, . So, one has, 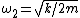
Since 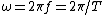 , the period , the period 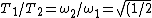/(2)}=1/2) , as in choice (A). , as in choice (A).
|
| 63 | Click here to jump to the problem! | GR8677 #4
|
Mechanics }Gravitational Law }Gravitational Law
Recall the famous inverse square law determined almost half a millennium ago,

where 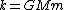 . .
The ratio of two inverse-square forces (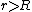 , where , where 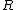 is the radius of the planet or huge heavy object) would be is the radius of the planet or huge heavy object) would be
}{F(r_2)}=\frac{4r_2^2}{r_1^2}.<br />
)
Thus, }{F(2R)}=\frac{4R^2}{R^2}=4) , which is choice (C). , which is choice (C).
|
| 64 | Click here to jump to the problem! | GR8677 #5
|
Mechanics }Gauss Law }Gauss Law
The inverse-square law doesn't hold inside the Earth, just like how Coulomb's law doesn't hold inside a solid sphere of uniform charge density. In electrostatics, one can use Gauss Law to determine the electric field inside a uniformly charged sphere. The gravitational version of Gauss Law works similarly in this mechanics question since 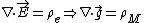 , where , where 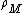 is the mass density of is the mass density of 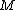 . In short, the gravitational field . In short, the gravitational field  plays the analogous role here as that of plays the analogous role here as that of  Thus, Thus, 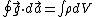 . .
So, for 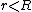 , , =\rho \frac{4}{3}\pi r^3 \Rightarrow g= r\frac{\rho}{3}) , where one assumes , where one assumes  is constant. is constant.
To express the usual inverse-square law in terms of  , one can apply the gravitational Gauss Law again for , one can apply the gravitational Gauss Law again for 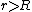 , , =\rho \frac{4}{3}\pi R^3 \Rightarrow g=\frac{R^3}{r^2}\frac{\rho}{3})
Since 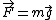 Therefore, Therefore,
}{F(R/2)}=2.
)
which is choice (C).
|
| 66 | Click here to jump to the problem! | GR8677 #7
|
Mechanics }Normal Modes }Normal Modes
For normal mode oscillations, there is always a symmetric mode where the masses move together as if just one mass.
There are three degrees of freedom in this system, and ETS is nice enough to supply the test-taker with two of them. Since the symmetric mode frequency is not listed, choose choice it!---as in (A).
|
| 69 | Click here to jump to the problem! | GR8677 #40
|
Mechanics }Centripetal Force }Centripetal Force
There is no tangential acceleration (since otherwise it would slide and not roll---the frictional force balances the forward acceleration force). However, there is a centripetal acceleration that pulls the particles back in a circle, as in choice (C). This acceleration propels the tangential velocity to continue spinning in a circle.
|
| 78 | Click here to jump to the problem! | GR8677 #78
|
Mechanics }Multiple Particles }Multiple Particles
The angular momentum equation gives the angular frequency. 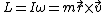 , which relates the angular momentum to the moment of inertia, the angular velocity, the radius of gyration and the linear velocity. , which relates the angular momentum to the moment of inertia, the angular velocity, the radius of gyration and the linear velocity.
The system spins about its center of mass, which is conserved. Since the pole is massless and the skaters are off the same mass, 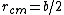 . The moment of inertia of the system is just . The moment of inertia of the system is just ^2) . .
Thus, the angular momentum equation gives ^2 \omega =m b/2 (v + 2v) \Rightarrow 2(b/2) \omega = 3v \Rightarrow \omega = 3v/b) , since the cross-products point in the same direction. Now that one has the angular velocity, one eliminates all but choices (B) and (C). , since the cross-products point in the same direction. Now that one has the angular velocity, one eliminates all but choices (B) and (C).
Now, take the time-derivative of x for choices (B) and (C), then evaluate it at 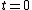 . .
For B, one has  \rightarrow 2.5v) for for 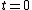 . .
For C, one has  \rightarrow 2v) for for 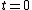 . .
Since the top skater is initially at =2v) , only choice (C) has the right initial condition. Choose choice (C). , only choice (C) has the right initial condition. Choose choice (C).
(FYI: The center of mass velocity is given by  . One can also arrive at (C) by noting conservation of center of mass velocity, since there is no net force.) . One can also arrive at (C) by noting conservation of center of mass velocity, since there is no net force.)
|
| 80 | Click here to jump to the problem! | GR8677 #87
|
Mechanics }Conservation of Energy }Conservation of Energy
Do not immediately try applying the Virial Theorem to this one. Instead, consider conservation of energy. Coming in from far away, the particle has 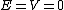 the total energy equal to the potential energy equal to 0. the total energy equal to the potential energy equal to 0.
Alternatively, one has, for a circular orbit, the equality between centripetal force and the attractive force, 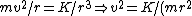) . .
Thus, the kinetic energy is just 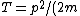 = K/(2r^2)) . .
Since 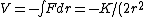) , where the extra negative sign for the potential energy is due to an attractive potential. , where the extra negative sign for the potential energy is due to an attractive potential.
Thus, the total energy 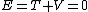 , which is choice (C). , which is choice (C).
(Alternate solution is due to user crichigno.) |
| 81 | Click here to jump to the problem! | GR8677 #93
|
Mechanics }Boundary Condition }Boundary Condition
Getting low on time, one should begin scoring points based more of testing strategy than sound rigorous physics. At the initial release point, the acceleration is due to gravity and the tension is 0 (no centripetal acceleration). The only choice that gives  = g) is choice (E). is choice (E).
|
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
