|
GR9677 #65
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
malxmusician212
2018-03-28 16:04:02 | you can also eliminate all the other answers by noting that as 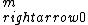 , the work required should approach infinity in a classical problem like this , the work required should approach infinity in a classical problem like this |  | exile
2014-10-16 23:37:34 | This question bothers me.
The work done is a result of the force applied, and because its really the boat that applied a force to the man, didn't the boat really do the work on the man (meaning the man did no work on himself, only work on the boat)? Or am I missing something?
I thought the test was trying to be tricky, but ironically I suppose in this question it was trying to be obvious.
ngendler
2015-10-23 05:01:55 |
That\'s what I thought too!
|
juxtaroberto
2017-07-23 08:01:08 |
But the boat only applied a force to the man because the man applied the force to the boat. Either way, energy is not a vector like momentum. The kinetic energies of the boat and the man don\'t cancel, the way their final momenta do. So, since the boat and the man started with zero kinetic energy, and both ended up with some kinetic energy, and the only energy source there is the man, he must have done all the work required to move himself forward and to move the boat back.\r\n\r\nThis also makes sense because as he jumps away, he\'s wasting some of his jump into pushing back against the boat, so the boat starts moving backward before his feet leave it, and that\'s some \"wasted\" energy that he expended but won\'t be propelling him forward. Thus the total work he does must be greater than his own kinetic energy.
|
|  | redmomatt
2011-09-23 14:05:09 | Slightly different angle.
Since m  = M v, we know that = M v, we know that  = Mv / m and = Mv / m and  > v. Therefore, the man must have a larger KE than the boat. We also see that there are two different denominators for > v. Therefore, the man must have a larger KE than the boat. We also see that there are two different denominators for 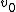 and v, so any addition of the two (Work-KE) will yield a total with both M and m somewhere. and v, so any addition of the two (Work-KE) will yield a total with both M and m somewhere.
Thus, looking at the answers, this leaves only (D).
redmomatt
2011-09-23 14:34:24 |
Just a note...
This should be the case for any M > m, so that the KE of m > KE of M (smaller mass => larger velocity for a given force, and since KE is dominated by 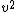 , the KE of the smaller object should be greater here). Thus, if they are represented by different symbols, you would expect to find an equation with M and m, where the KE of m > KE of M. , the KE of the smaller object should be greater here). Thus, if they are represented by different symbols, you would expect to find an equation with M and m, where the KE of m > KE of M.
In this case, again, this leaves only (D).
|
|  | walczyk
2011-03-31 13:07:05 | here's a fast way to think this through. don't be scared when you see work, because you'll remember the work-kinetic energy theorem and know that this is what the problem is asking.
So work is equal to the change of kinetic energy, as written in the solution above. so write it out, and THEN apply conservation of momentum to eliminate 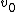 . Doing things in this order just keeps you from getting confused. . Doing things in this order just keeps you from getting confused. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
