ernest21
2019-08-23 02:01:45 | Another way to understand that it\'s the first normal mode is that the same boundary conditions have the same solutions: if the center mass is still, each other mass may as well be attached to a wall. ruff ruffman games |  |
joshuaprice153
2019-08-09 06:11:13 | I think this is one of the best source. I have found what I was looking for. A good day. appliance repair St Petersburg |  |
joshuaprice153
2019-08-09 06:10:36 | I think this is one of the best source. I have found what I was looking for. A good day appliance repair St Petersburg |  |
apg
2016-09-16 08:53:41 | this problem is lot simpler if we consider L to be very small ( point object) \r\nso from conservation of momentum during the collision of two particles\r\n \r\nmv= m * 0( since after collision mass is at rest) + MV \r\nmv= MV\r\nV=mv/M\r\n\r\nwhich easily gives the option A\r\n |  |
calvin_physics
2014-03-27 23:14:30 | So Here's what I did,
Denoting linear velocity of particle = v
Denoting linear velocity of rod after collision = u
Conservation of Linear momentum:
mv = Mu
(m/M)v = u
Conservation of Angular momentum
mv(L/2) = (1/12)ML*Lw
w = 6*m*v/(ML)
Conservation of Energy
mv*v = M*u*u + I*w*w
I found that M has to be 4m in order for elastic collision to happen. Is this true?
|  |
calvin_physics
2014-03-27 16:29:20 | So you are saying if m = M, the rod does not spin?
That is quite counter intuitive. |  |
849444209
2013-10-16 06:27:08 | 这道题太尼玛简单了!!!!!!ETS大笨蛋!!!!
rahat90
2014-09-07 10:14:41 |
也许你太天才还是一个大嘴巴的恶棍 ! ! !
|
|  |
gigadan
2013-09-23 21:28:30 | if angular momentum and linear momentum conserved...
then the only condition that would make it elastic is that m = M ...
Correct me if I'm wrong on this one... |  |
gigadan
2013-09-23 21:19:46 | So are angular momentum and linear momentum conserved at the same time here?rnrnlinear momentum => mv = MV rnangular momentum = (2v/L)*m(L/2)^2 = w*(1/12)ML^2 |  |
walczyk
2011-03-08 23:53:47 | I see some people are confused about the energy approach here. It is only of use after you use the given information to deduce the linear momentum and linear kinetic energy of the rod, so that you can solve the angular frequency in terms of v alone.
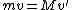

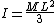
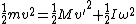
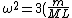^2 (\frac{M}{m} - 1)v^2)
There you have it folks, including what happens at  . .
Manuel Abad
2012-01-18 11:23:28 |
Actually you made a mistake in the expression for the moment of inertia of the rod: it is
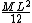 , not , not 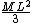
Also, I am worried. Yes, I know they're not asking for the angular momentum or angular velocity... but while obtaining  , which is: , which is:
})
and then asking for the conservation of angular momentum (with respect to a point located at the stick's center), I get that the initial angular momentum is:
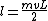
and the final must be:
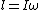
and, equating both of these expressions (because of the conservation of angular momentum) I get that they're only equal if and only if:
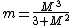
What could this mean? Where am I wrong? Please, Help!!
|
twd
2012-10-24 18:15:08 |
In a problem like this, in general, there would be three equations (linear momentum, energy, angular momentum) and three unknowns (final velocity of the ball, angular velocity of stick, COM velocity of stick), so we should be able to solve for all three quantities uniquely. However, you are given an extra piece of information here (the particle is at rest after collision), so you naturally expect to be able to eliminate one more variable and get a relationship between 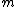 and and 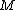 which conserves everything. which conserves everything.
|
walczyk
2012-11-10 04:24:27 |
I just looked at my solution again and it is wrong because I assume it is an elastic collision. The real answer is
^2\frac{1}{1+\frac{m}{M}}) where where  is a constant is a constant  which handles the distance from the rod's center that the ball makes contact. Obviously this is totally unnecessary because the question is asking for the speed of the center of mass. which handles the distance from the rod's center that the ball makes contact. Obviously this is totally unnecessary because the question is asking for the speed of the center of mass.
|
walczyk
2012-11-10 04:43:01 |
I noticed, it DOES say it is elastic, anyway my solution is still correct. Doing it using energy is much more difficult, because one of the steps (in either approach) is to calculate the angular momentum of the particle the moment before it strikes. The center of mass of the system at this moment is 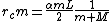 so so  and right after collision we have and right after collision we have 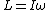 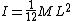 . As you can see, using the energy approach you'd have a rotational energy term on either side, bascially a mess. (note I forget a factor of v in my calculation of angular frequency in an earlier post. . As you can see, using the energy approach you'd have a rotational energy term on either side, bascially a mess. (note I forget a factor of v in my calculation of angular frequency in an earlier post.
|
beruni
2013-02-17 09:37:00 |
Where aren't you considering the initial angular momentum of the mass, which is 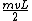 ? ?
|
|  |
padkins
2011-02-06 11:52:55 | If you do the same equation using conservation of energy you get Vstick = v*sqrt[(m/M)-3(m/M)^2]. This apparently means that elastic collision is impossible for m/M<1/3 if the ball is to stand still after collision.
If we use both conservation of energy given the fact that it is an elastic collision ANNND we use conservation of linear momentum, we find the condition for the collision to be elastic and for the ball to stand still afterwards is that m/M=1/4. |  |
ProofbyInspection
2010-11-12 17:30:53 | I'm pretty sure energetic methods (as suggested in the solutions) would fail here, considering energy is not generally conserved in collisions.
pam d
2011-09-24 11:08:16 |
No they will not because the problem states that the collision is elastic.
|
|  |
ramparts
2009-11-05 11:30:23 | Minor trick for those of us not physics-savvy enough to realize that the angular stuff is unimportant: even if you're worried that rotational effects will come into play, in this problem ETS is extremely generous to not give any answers involving L. You know that if the rod were a point particle (L goes to 0) the answer is (A), so since none of the answers have L-dependence and can't achieve that limit, it's got to be (A). |  |
segfault
2009-08-25 20:05:23 | Is it true that for this situation to occur 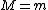 ? (Because the point particle comes completely to rest after the collision) ? (Because the point particle comes completely to rest after the collision)
wittensdog
2009-09-28 20:03:20 |
I don't think so, not in this case.
The requirement that m = M for the first one to come to rest is when you have two point particles hitting each other head on. The fact that m = M comes from the requirement that kinetic energy and momentum both be conserved.
However, in this problem, kinetic energy is not necessarily conserved. Well, technically it is, but that's if you call the sum total of the rotation of all of the little atoms inside as part of the kinetic energy. So what happens is that the first particle has some kinetic energy, which then goes into kinetic energy of the center of mass of the stick and rotational energy of the stick. To know how much energy goes into the translation of the center of mass and how much goes into rotation, you'd need to know the moment of inertia. I guess you could look up what it would be for a uniform spatially extended stick, but I think the point remains that if you had an object with the right combination of mass and moment of inertia, the mass need not be the same as the incoming particle to bring it to rest.
Then again I could be wrong, I didn't verify this rigorously, just kind of reasoned it out in my head.
|
shafatmubin
2009-10-31 19:54:10 |
If the problem is worked out in detail, it turns out that M = m indeed:rnrnM = m [ (v - 0) / (v + 0)] -> M = mrnORrnvFinalOfm = 0 = [(m - M) / (m + M) ] v -> m = M
|
|  |
eliasds
2008-11-02 14:36:44 | I'm still confused. the equation ) =MV in no way shows the linear momentum of the particle contributing to the new angular momentum of the stick. Can someone clearly explain why angular momentum does not show up in the equation? =MV in no way shows the linear momentum of the particle contributing to the new angular momentum of the stick. Can someone clearly explain why angular momentum does not show up in the equation?
OrrinJelo
2009-09-24 19:01:08 |
Think of it as this: Linear momentum of the particle contributes to the linear momentum of the stick; the angular momentum of the particle contributes to the angular momentum of the stick.
How can the particle have angular momentum? Let me point out first that the particle hits the end of the stick, not at the center (where the center of mass is). If we look at the angular momentum about the center of mass of the stick, of course the particle has angular momentum! If you do the math, it will work out.
|
|  |
phys2718
2008-10-16 13:54:11 | I think the crucial point here is that the rod is a rigid body; thus all parts of the rod rotate about the center with the same frequency, and the linear momentum of one side of the rod due to the rotation is completely canceled by the momentum of the other side. So only the linear momentum of the center of mass needs to be taken into account. |  |
sabinscabin
2008-10-15 21:51:31 | I kept seeing the word "stick" in the problem; it is mentioned 4 times. So I thought that the mass "sticks" to the rod, which made me pick B.
D'oh!!!!!
511mev
2009-11-02 13:41:54 |
That's hilarious!
|
Setareh
2011-10-25 14:10:58 |
:))))))))) Funny
|
Lilia
2012-08-28 18:16:04 |
Wow, I'm not alone! :D
|
|  |
Rune
2007-10-13 23:05:52 | I'm a bit confused because it seems to me that if the surface is frictionless and you hit a rod at one end, some of the momentum would go to rotating the rod. Why doesn't this happen?
jsdillon
2008-04-11 19:48:56 |
It does rotate. However, since the problem is asking for the velocity of the center of mass of the stick, it doesn't matter. The solution of the problem doesn't require a consideration of the conservation of angular momentum (although it is, indeed, conserved)--conservation of linear momentum is plenty.
|
p3ace
2008-05-04 14:34:50 |
Only linear momentum for center-of-mass coordinates is needed.
|
anum
2010-11-11 10:26:06 |
in a rotational motion center of mass of the body is still in a linear motion.
|
Almno10
2010-11-11 21:03:34 |
The ang. mom. of the particle does rotate the stick. The angular momentum of the particle is m(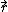 x x 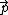 ) which will be conserved. But who cares about that? It asks for linear momentum. ) which will be conserved. But who cares about that? It asks for linear momentum.
Think of the particle hiting the center of the stick. No rotation, baby.
|
|  |
grscjo3
2006-11-03 21:01:37 | When you say that by using energy to solve this, one would have to take into account the inertia, do you mean the rotational inertia of the rod?
yosun
2007-02-22 15:11:24 |
Yes, referring to this kind of inertia: 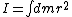
|
|  |
