|
GR8677 #43
|
|
|
Problem
|
|
 |
Mechanics }Normal Modes }Normal Modes
Because there are two degrees of freedom in this problem, there are two normal mode frequencies.
Because there is no external torque acting on the system, the center of mass of the system stays the same through time.
From common sense, one deduces that 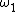 has to do with the outer masses moving perfectly out of phase, i.e., masses A and C moving either towards the left and right (away from each other), respectively, or right and left (towards each other), respectively---and B being perfectly stationary, thereby ``conserving" the center of mass. has to do with the outer masses moving perfectly out of phase, i.e., masses A and C moving either towards the left and right (away from each other), respectively, or right and left (towards each other), respectively---and B being perfectly stationary, thereby ``conserving" the center of mass.
The other angular frequency,  , has to do with either masses A and C moving in phase and mass B out of phase. , has to do with either masses A and C moving in phase and mass B out of phase.
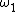 is actually equivalent to having a single mass on a string, since because the middle mass doesn't move, it acts as a sort of support for the spring. is actually equivalent to having a single mass on a string, since because the middle mass doesn't move, it acts as a sort of support for the spring. 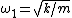 , which would correspond to choice (B). (Of course, one should recall the obvious, that , which would correspond to choice (B). (Of course, one should recall the obvious, that 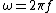 .) .)
(Incidentally, one can derive  without having to resort to the formalism of matrix mechanics: Since the center of mass remains 0, one has without having to resort to the formalism of matrix mechanics: Since the center of mass remains 0, one has 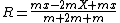 . Solving, one gets . Solving, one gets 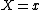 . The displacement of the middle mass, mass B, is thus . The displacement of the middle mass, mass B, is thus 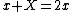 , while the displacements of the smaller masses, masses A and C, are both , while the displacements of the smaller masses, masses A and C, are both  . The displacement of each spring is . The displacement of each spring is 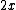 . Potential energy is thus . Potential energy is thus ^2=\frac{1}{2}8kx^2) . The kinetic energy is . The kinetic energy is ^2+\frac{1}{2}(2m)(\dot{x})^2=\frac{1}{2}4m(\dot{x})^2) . The normal mode frequency is deduced by . The normal mode frequency is deduced by 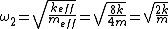 ) )
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ernest21
2019-08-23 02:01:26 | I always used to get confused over cross section problems because I had a hard time conceptually understanding what it meant. I think part of the issue was that in problems like these, I would want to ask \"scatter by how much of an angle?,\" or I would get concerned over the particulars of what a scattering event was. police pursuit game |  | joshuaprice153
2019-08-09 05:37:19 | You put really very helpful information. Keep it up. Keep posting. Looking to reading your next post. sprinkler repair Tampa |  | SarlCagan
2016-10-27 16:53:54 | If the centre particle B isn\'t moving, then you can think of it as a wall. Then A and C don\'t know about each other, and will each independently oscillate as if they were simple oscillators, with frequency 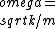 \r\n\r\nSo the answer is choice B (which in this case is the only one that has particle B at rest) \r\n\r\nSo the answer is choice B (which in this case is the only one that has particle B at rest) |  | novice
2011-11-09 17:48:24 | Why isn't it C or D? |  | fpaslan
2011-11-02 15:23:13 | In a two mass point coupled system, there are two normal modes. The one with higher frequency corresponds to the motion in opposite phase. The frequency is lower when the mass points are in phase. In this system the number of normal modes is three. The first one; w=0, there is no vibration but translation. Second (k/m); the mass between is at rest. Third (2k/m) the mass between is in opposite phase with the others, and if we take the system two by two, the near mass points are in opposite phase with higher frequency. So we can apply the same lower frequency >in phase and higher frequency> in opposite phase rule if we take the mass points two by two. |  | Setareh
2011-10-25 13:56:57 | According to what I learnt from professor Walter Lewin, I think the number of normal modes depends on the number of masses, not the degree of freedom. One normal mode should be zero.
Israel.cma
2013-03-02 11:32:12 |
The number of normal modes does depend on the number of degrees of freedom. For example, the number of modes would be different if we consider up and down motion (transverse modes), while the number of masses remains the same. Nevertheless, I agree with you, there is and extra trivial normal mode that equals zero, that happens when there is no vibration, all the masses moves with the same speed.
|
|  | evanb
2008-06-19 22:30:48 | Another way to understand that it's the first normal mode is that the same boundary conditions have the same solutions: if the center mass is still, each other mass may as well be attached to a wall.
Then, we know immediately that the spring / mass system oscillates with frequency 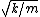 . .
Inspired by e/m problem of a point charge and an infinite conducting plane: may as well ditch the plane and add an image charge.
neon37
2010-11-01 12:34:59 |
I did the problem the same way but the e/m analogy is excellent! Thanks.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
