|
GR8677 #42
|
|
|
|
|
Alternate Solutions |
ramparts
2009-10-30 15:36:46 | Wow. All these answers have WAY too much physics. The chances of there being some law of physics in which dimensionless constants change your answer by a factor of 2 or so is really small, and all of your answers are off by at least a factor of 2. So look at dimensions.
You want an answer in cm^2. You have quantities in cm and cm^3. One of them is actually nuclei/cm^3, and you have another thing involving nuclei (1/10^6, one in a million). There's only one way to combine those first two to get something with the right dimensionality for cm, then you also multiply by the 1 in a million term to get rid of the nuclei units:
10^-20 * 1/0.1 * 10^-6 = 10^-25.
QED folks.
Order of magnitudes. They work. |  | wittensdog
2009-08-05 07:08:14 | Scattering cross sections was always an area (no pun intended) I particularly disliked, so I figured I would post some information that helped me out.
Tom Kibble's book on classical mechanics really helped me out, in particular section 4.6, where it discusses the mean free path. You can find the fifth edition on Google Books:
http://books.google.com/books?id=0a8dk0eDxgEC&printsec=frontcover&dq=classical+mechanics#v=onepage&q=&f=false
I highly suggest reading through that section. Also, there is some information on Wikipedia:
http://en.wikipedia.org/wiki/Mean_free_path
I generally feel more comfortable with a subject when I understand where it comes from, so seeing how the scattering formula was built up from the idea of mean free path helped me a great deal. Of course, on the test I will not go and derive the result, but I think it helps you have a better sense of whether or not you're using the right formula in the right situation. The following is how I approached this problem, with the above information in mind.
For reasons that are explained very well in Kibble's book, the mean free path of a particle, that is, the average length between collisions, will be given by l = (n * a) ^ -1, where n is the number density of targets, in this case some sort of nuclei, and a is the cross sectional area presented by the each nuclei. Now, if you follow the derivation on either the Wikipedia article, or in Kibble's book, you find that the fraction of transmitted particles through a target of thickness x will be T = exp(-x/l).
It turns out that the mean free path l for any of the possible choices of cross section would result in a value of x/l that is no more than 0.01, so the argument of the exponent is very small. This allows for the first order Taylor expansion T = 1 - x/l. The fraction of scattered particles will be S = 1 - T, or x/l. Remembering the formula for the mean free path, we end up with:
S = x*n*a
So in the limit that the thickness of the target is small in comparison with the mean free path for collisions, the fraction of scattered particles is just the thickness of the target, multiplied by the number density of targets and the cross sectional area presented by each. In the event that ETS wanted to be particularly brutal, I guess knowing the exponential formula could help in the event that the target was not thin in comparison with the mean free path.
I always used to get confused over cross section problems because I had a hard time conceptually understanding what it meant. I think part of the issue was that in problems like these, I would want to ask "scatter by how much of an angle?," or I would get concerned over the particulars of what a scattering event was. But I realize now that in general, when you ask about a cross sectional area, what it means is, what effective area does a target present that will cause the incident particle to scatter into some particular region or solid angle of interest. So calculating the cross sectional area from first principles, and not an experiment as in this problem, would indeed require some knowledge of the interactions involved, and the cross section would be a function of what region you were talking about. But, when no mention is made as to what scattering region is in question, or what it is that constitutes a scattering event, from what I can tell, it is implied that we have some unspoken definition of what constitutes a "scattering," and the cross sectional area we are talking about is assumed to mean the effective area that the incident particle must come within around the target to scatter in a way that we consider to be a "scattering event."
Anyways, I hope this helps someone. |  | eshaghoulian
2007-09-15 15:45:00 | If you assume linearity in the variables and their inverses (and that there are no constants up front), then there is a unique solution. By looking at the answer choices, you can deduce that it must go as 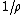 . Since the answer is in . Since the answer is in 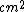 , it must also go as , it must also go as 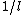 . So we have . So we have  . It must, then, depend linearly on the final variable, P, to give you an answer choice in the list. . It must, then, depend linearly on the final variable, P, to give you an answer choice in the list.
I guess this method is good if you remember seeing a formula that was linear in all its variables (or inverse variables), which would probably be applicable to a very small subset of people. However, on the GRE, I would suggest making this assumption if you have no other way of solving the problem. The answer choices are begging you to. Besides, you'd probably have to come up with a complicated formula (remember that you have to get the units right too, so squaring 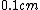 gives you gives you  , and you have to fix for this somewhere else in your formula) to land on one of the answer choices, especially because it says "the scattering cross section is" and not "the scattering cross section is approximately" (this rules out constants that aren't exactly , and you have to fix for this somewhere else in your formula) to land on one of the answer choices, especially because it says "the scattering cross section is" and not "the scattering cross section is approximately" (this rules out constants that aren't exactly 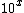 for integer for integer  ). ). |  |
|
|
Comments |
ernest21
2019-08-23 02:00:39 | Fortunately for us, Iron (C) is \'clearly\' the only choice in this band. No doubt there\'s actually a relation defining this curve. (somewhere) android oreo easter egg |  | joshuaprice153
2019-08-09 05:26:02 | Nice post, that was exactly i was looking for today. Informative air duct cleaning Miami |  | buaasyh
2015-09-07 09:16:03 | The scattering cross section is about the nuclei in the scatterer. On average, one nucleus share an area of (1 cm^3)/(0.1 cm×10^20)=10^-19 cm^2. However, the nucleus does not cover the whole part of the average area, or the probability of the protons hitting a nucleus would be 1 instead of 1 in a million. Thus the nucleus only occupies 1 millionth of the average area, that is 10^-19/10^-6=10^-25 cm^2. |  | mpdude8
2012-04-15 21:47:46 | Agreed with ramparts. Without ever invoking any knowledge of physics whatsoever:
You have something given as 0.1 cm. You have something else given as 10^20 1/(cm^3). You're asked to find something that has units cm^2. So, multiply 10^20 cm^-3 by 0.1 cm five times to get something with cm^2 as its units. Only possibility is C.
Who's gonna have time to invoke all this stuff about scattering and whatnot when you only have 1-2 minutes per question? |  | ramparts
2009-10-30 15:36:46 | Wow. All these answers have WAY too much physics. The chances of there being some law of physics in which dimensionless constants change your answer by a factor of 2 or so is really small, and all of your answers are off by at least a factor of 2. So look at dimensions.
You want an answer in cm^2. You have quantities in cm and cm^3. One of them is actually nuclei/cm^3, and you have another thing involving nuclei (1/10^6, one in a million). There's only one way to combine those first two to get something with the right dimensionality for cm, then you also multiply by the 1 in a million term to get rid of the nuclei units:
10^-20 * 1/0.1 * 10^-6 = 10^-25.
QED folks.
Order of magnitudes. They work.
flyboy621
2010-11-14 20:32:04 |
^ this
|
Nezumi
2013-07-11 17:09:13 |
Nice.
|
|  | wittensdog
2009-08-05 07:08:14 | Scattering cross sections was always an area (no pun intended) I particularly disliked, so I figured I would post some information that helped me out.
Tom Kibble's book on classical mechanics really helped me out, in particular section 4.6, where it discusses the mean free path. You can find the fifth edition on Google Books:
http://books.google.com/books?id=0a8dk0eDxgEC&printsec=frontcover&dq=classical+mechanics#v=onepage&q=&f=false
I highly suggest reading through that section. Also, there is some information on Wikipedia:
http://en.wikipedia.org/wiki/Mean_free_path
I generally feel more comfortable with a subject when I understand where it comes from, so seeing how the scattering formula was built up from the idea of mean free path helped me a great deal. Of course, on the test I will not go and derive the result, but I think it helps you have a better sense of whether or not you're using the right formula in the right situation. The following is how I approached this problem, with the above information in mind.
For reasons that are explained very well in Kibble's book, the mean free path of a particle, that is, the average length between collisions, will be given by l = (n * a) ^ -1, where n is the number density of targets, in this case some sort of nuclei, and a is the cross sectional area presented by the each nuclei. Now, if you follow the derivation on either the Wikipedia article, or in Kibble's book, you find that the fraction of transmitted particles through a target of thickness x will be T = exp(-x/l).
It turns out that the mean free path l for any of the possible choices of cross section would result in a value of x/l that is no more than 0.01, so the argument of the exponent is very small. This allows for the first order Taylor expansion T = 1 - x/l. The fraction of scattered particles will be S = 1 - T, or x/l. Remembering the formula for the mean free path, we end up with:
S = x*n*a
So in the limit that the thickness of the target is small in comparison with the mean free path for collisions, the fraction of scattered particles is just the thickness of the target, multiplied by the number density of targets and the cross sectional area presented by each. In the event that ETS wanted to be particularly brutal, I guess knowing the exponential formula could help in the event that the target was not thin in comparison with the mean free path.
I always used to get confused over cross section problems because I had a hard time conceptually understanding what it meant. I think part of the issue was that in problems like these, I would want to ask "scatter by how much of an angle?," or I would get concerned over the particulars of what a scattering event was. But I realize now that in general, when you ask about a cross sectional area, what it means is, what effective area does a target present that will cause the incident particle to scatter into some particular region or solid angle of interest. So calculating the cross sectional area from first principles, and not an experiment as in this problem, would indeed require some knowledge of the interactions involved, and the cross section would be a function of what region you were talking about. But, when no mention is made as to what scattering region is in question, or what it is that constitutes a scattering event, from what I can tell, it is implied that we have some unspoken definition of what constitutes a "scattering," and the cross sectional area we are talking about is assumed to mean the effective area that the incident particle must come within around the target to scatter in a way that we consider to be a "scattering event."
Anyways, I hope this helps someone.
walczyk
2011-03-09 00:14:05 |
awesome
|
kronotsky
2018-10-23 04:11:55 |
I really wish that every QFT/particle physics class spent like one or two whole lectures on the cross section right at the beginning.\r\n\r\nAs to the \"particularly brutal\" part, the essential reason why the formula is exponential is that the probability of multiple collisions along an initial trajectory becomes non-trivial in the limit of higher densities. By the problem statement, we are in the limit of low *single* collision probability, so the probability for scattering is proportional to the thickness of the sample. It is also inversely proportional to the density. This is the essential information you need to know to solve the problem (without dimensional analysis, which you should definitely use).
|
|  | jw111
2008-09-01 14:42:52 | Let's forget about Scattering Cross Section a moment, and image a fish who want to swim across the pool with half of it's cross section with a net.
If the fish is blind, the chance of the fish to reach the other end of the pool is clearly 50%. You get this answer by
the area of the net/total area(cross section) of pool = 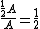
Let's go back to Scattering Cross Section.
DEFINITION :
If a SINGLE nuclei can hold a net on it' hand (if it has) to catch the proton, the Scattering Cross Section is just the area of the net !
S0 for protons passing through this pool (the scatterer)
the chance 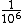 = sum of total area of net/total area of pool = = sum of total area of net/total area of pool =
volume*density*cross section/area =
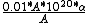
so the  is the answer. is the answer.
jw111
2008-09-01 14:52:31 |
correction
0.1 (not 0.01)
|
phys2718
2008-10-16 12:03:24 |
This is the most incomprehensible explanation I have ever read. Yes, lets "image a fish who want to swim across the pool".
|
neon37
2008-11-02 21:45:09 |
I guess this analogy was good for ppl like me who mistook the scattering cross-section with the cross-section area.
|
|  | petr1243
2008-03-08 15:37:10 | Just remember that probablility P= R/R0 is:
P=( )(nAx)/A = ( )(nAx)/A = ( )(nx) giving us: )(nx) giving us:
cross section  = P/nx = P/nx |  | eshaghoulian
2007-09-15 15:45:00 | If you assume linearity in the variables and their inverses (and that there are no constants up front), then there is a unique solution. By looking at the answer choices, you can deduce that it must go as 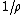 . Since the answer is in . Since the answer is in 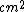 , it must also go as , it must also go as 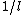 . So we have . So we have  . It must, then, depend linearly on the final variable, P, to give you an answer choice in the list. . It must, then, depend linearly on the final variable, P, to give you an answer choice in the list.
I guess this method is good if you remember seeing a formula that was linear in all its variables (or inverse variables), which would probably be applicable to a very small subset of people. However, on the GRE, I would suggest making this assumption if you have no other way of solving the problem. The answer choices are begging you to. Besides, you'd probably have to come up with a complicated formula (remember that you have to get the units right too, so squaring 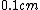 gives you gives you  , and you have to fix for this somewhere else in your formula) to land on one of the answer choices, especially because it says "the scattering cross section is" and not "the scattering cross section is approximately" (this rules out constants that aren't exactly , and you have to fix for this somewhere else in your formula) to land on one of the answer choices, especially because it says "the scattering cross section is" and not "the scattering cross section is approximately" (this rules out constants that aren't exactly 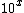 for integer for integer  ). ). |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
