casseverhart13
2019-09-27 02:58:26 | Well this is a real life-saver! commercial cleaning |  |
joshuaprice153
2019-08-09 03:07:39 | With more intentions to get back to your answer, i was annoyed last week when i didn\'t even got time to read anything over internet. mobile window tinting |  |
TimToolMan
2018-04-03 00:15:02 | Simple Unit argument.\\\\r\\\\nEnergy is in units of ) \\\\r\\\\nSo we can get the units of k to be \\\\r\\\\nSo we can get the units of k to be ) \\\\r\\\\nForce must be in units of \\\\r\\\\nForce must be in units of ) \\\\r\\\\nKeeping k\\\\\\\'s units in mind, there are only 2 solutions with these units of force: B & E\\\\r\\\\nNo gravity in this question, so it must be B \\\\r\\\\nKeeping k\\\\\\\'s units in mind, there are only 2 solutions with these units of force: B & E\\\\r\\\\nNo gravity in this question, so it must be B |  |
OrrinJelo
2009-08-04 10:37:53 | The easiest way is by doing dimensional analysis. (A) is in units of energy, same with (C). (D) is energy times distance. This leaves (B) and (E). (E) is the force associated with gravity, which our potential energy equation looks nothing like the gravitational potential equation. We are left with (B).
neon37
2010-11-01 10:42:12 |
I think thats the hardest way to do this. Easiest is the solution given. You should remember that 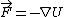 . If you dont then you should think about memorizing that one. It will be mighty helpful. . If you dont then you should think about memorizing that one. It will be mighty helpful.
|
pam d
2011-09-24 09:53:55 |
neon37, I second that.
|
mpdude8
2012-04-15 21:03:04 |
Even though that's the long route for this problem, knowing the units of "k" will be useful in 35 and 36.
|
|  |
jitin1984
2006-10-27 15:15:32 | hey
i cant get enough practice problems for quant. i have got schaum seeries but it has only derivations any one has any material plz i want it |  |
Mexicorn
2005-11-08 12:10:14 | I think you mean 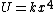 instead of instead of 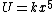 for the potential given. for the potential given.
yosun
2005-11-09 02:27:05 |
Mexicorn: thanks for the typo-alert; it has been corrected.
|
|  |
