|
GR9277 #41
|
|
|
|
|
Alternate Solutions |
Ryry013
2019-10-06 09:10:04 | A slightly faster way to do this problem is to know that if omega halves, then kinetic energy will decrease by 1/4. Then energy LOST is just (0.5)(4)(80^2) * (3/4) = (0.5)(6400)(3/4) = 9600J |  |
|
|
Comments |
Ryry013
2019-10-06 09:10:04 | A slightly faster way to do this problem is to know that if omega halves, then kinetic energy will decrease by 1/4. Then energy LOST is just (0.5)(4)(80^2) * (3/4) = (0.5)(6400)(3/4) = 9600J |  | mnky9800n
2013-09-24 13:05:47 | I also like to think in terms of the potential energy of a 100kg person who is about to fall 10 meters. That is mgh~(100 kg)(10 m/s^2)(10 m) = 10000 J. Thus A and B are probably too small and E is probably too big. |  | aloha
2008-10-10 03:21:51 | Maybe it's a silly question, but how can we know that I=4?
Thanks :)
Monk
2008-10-13 20:11:46 |
it tells you in the question...it is 4 kg m^2
kg m^2 is the units not a formula
|
tensordyne
2008-11-04 13:16:28 |
I am with Monk, from reading the problem it seems like they are saying 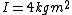 is a formula in k (proportionality factor maybe), g ( is a formula in k (proportionality factor maybe), g (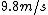 ) and mass m instead of as units because there is no grouping of the units, such as in say ) and mass m instead of as units because there is no grouping of the units, such as in say 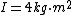 , which would have made the use of units much more manifest. , which would have made the use of units much more manifest.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
