\prob{42}
A cylinder with moment of inertia 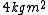 about a fixed axis initially rotates at 80 radians per second about this axis. A constant torque is applied to slow it down to 40 radians per second. about a fixed axis initially rotates at 80 radians per second about this axis. A constant torque is applied to slow it down to 40 radians per second.
If the cylinder takes 10 seconds to reach 40 radians per second, the magnitude of the applied torque is
- 80 Nm
- 40 Nm
- 32 Nm
- 16 Nm
- 8 Nm
|
Mechanics }Angular Kinematics }Angular Kinematics
Kinematics with angular quantities is exactly like linear kinematics with
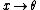 (length to angle) (length to angle)
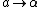 (linear acceleration to angular acceleration) (linear acceleration to angular acceleration)
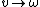 (linear velocity to angular velocity) (linear velocity to angular velocity)
 (mass to moment of inertia) (mass to moment of inertia)
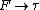 (force to torque). (force to torque).
Thus, one transforms 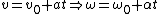 . .
Plugging in the given quantities, one gets 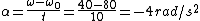 . .
The torque is given by 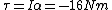 , whose magnitude is given by choice (D). , whose magnitude is given by choice (D).
|
