GREPhysics.NET: GR9277 #45

GR9277 #45

Problem

GREPhysics.NET Official Solution

\prob{45}
A ball is dropped from a height h. As it bounces off the floor, its speed is 80 percent of what it was just before it hit the floor. The ball will then rise to a height of most nearly

0.94 h
0.80 h
0.75 h
0.64 h
0.50 h

Mechanics $\Rightarrow$ }Conservation of Energy

Conservation of energy gives $mgh = \frac{1}{2}mv_0^2$ , where $v_0$ is the velocity of the ball before it strikes the ground. Thus, $v_0^2 = 2gh$ .

Afterward, the ball bounces back up with $v^{'}=0.8v$ . Apply conservation of energy again to get $mgh^{'} = \frac{1}{2}mv^{'2} \Rightarrow v^{'2} = 2gh^{'} \Rightarrow h^{'}=v^{'2}/(2g)$ .

Plugging in $v^{'2}=0.8^2v_0^{2}$ , one has $h^{'}=0.64h$ , which is choice (D).

Alternate Solutions

QuantumCat
2014-09-01 12:35:26

The first thing I noticed was that it lost 64% of its kinetic energy, so it will only rise to 64% of it's original height. Even though it's a bit of a rehash from everything that has been mentioned, this solution solves the problem in just a few seconds.

Reply to this comment

Comments

QuantumCat
2014-09-01 12:35:26

ETScustomer
2017-09-22 20:06:10

It kept* 64 percent of its kinetic energy.

Reply to this comment

myscifilullaby
2012-04-03 13:59:07

quickest way. Use ratios while also noting matweiss's comment:

h/(v^2)=x/((0.8v)^2)

x=(0.8^2)h=0.64h

Reply to this comment

matweiss
2010-11-13 18:11:12

This is something everyone should know:

The height that an object rises to is proportional to the square of V/V(initial)

Example: if ball A is thrown up in the air at v= 100 m/s and ball B is thrown up in the air at 10 m/s what is the ratio of the height ball A will reach to the height ball B will reach.

the answer is (100/10)^2 = 100. Aka, ball A will go 100 times as high as ball B. If you don't believe me you can do the math out yourself, if you do, hopefully it'll be the last time you work it out this way.

Reply to this comment

ramparts
2009-08-09 20:45:30

The quicker way to do this is to work entirely with energies (just skips a couple of steps):

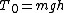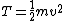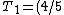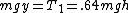$T_0 = mgh$ is the kinetic energy at the ground. Some amount of kinetic energy is lost there - since $T = \frac{1}{2} m v^2$ , we have $T_1 = (4/5)^2 T_0$ . (4/5)^2 is .64, so 36% of the energy is lost. So by conservation of energy again, with y as the height the ball reaches, $mgy = T_1 = .64 mgh$ . $y = .64 h$ . Simple as that ;)

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone