|
GR0177 #55
|
|
|
|
|
Alternate Solutions |
carle257
2010-04-01 20:20:09 | This can be done simply by acknowledging that the x momentum is conserved so  . Then if they also have a vertical component, the speed must be greater than this value. Thus the answer must be (E). . Then if they also have a vertical component, the speed must be greater than this value. Thus the answer must be (E). |  |
|
|
Comments |
shka
2018-07-08 19:07:34 | carle257 is using symmetry instead of explicitly writing out the equations for 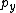 and and 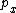 conservation. His answer is fine and consistent with Yosun\'s, and the fact that Quark is confused by the notation conservation. His answer is fine and consistent with Yosun\'s, and the fact that Quark is confused by the notation 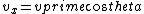 makes me think he doesn\'t understand how right triangles work. You can ALWAYS solve for the components of the velocity, by definition of linear momenta makes me think he doesn\'t understand how right triangles work. You can ALWAYS solve for the components of the velocity, by definition of linear momenta  and and 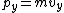 , and since , and since 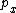 and and 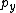 are conserved separately. Whether or not you choose to fuss with the angles is completely up to you. Since the angles and masses are identical, if you paid attention in PHYS 100 you can literally just read off the answer. Thanks Quark, for obfuscating a perfectly good solution with your utter misunderstanding of first principles. Maybe you should crack open Giancoli a few more times before applying to CERN, since I\'m pretty sure they like to conserve momentum linear momentum there. are conserved separately. Whether or not you choose to fuss with the angles is completely up to you. Since the angles and masses are identical, if you paid attention in PHYS 100 you can literally just read off the answer. Thanks Quark, for obfuscating a perfectly good solution with your utter misunderstanding of first principles. Maybe you should crack open Giancoli a few more times before applying to CERN, since I\'m pretty sure they like to conserve momentum linear momentum there. |  | aziza
2014-08-12 12:59:18 | If you run the collision backward in time, you see it as two objects mass m combining into one of mass 2m, so this is inelastic. Thus the final kinetic energy of the system should be greater than initial, giving each of the two masses velocity > v/2 . |  | carle257
2010-04-01 20:20:09 | This can be done simply by acknowledging that the x momentum is conserved so  . Then if they also have a vertical component, the speed must be greater than this value. Thus the answer must be (E). . Then if they also have a vertical component, the speed must be greater than this value. Thus the answer must be (E).
Quark
2011-09-26 16:36:49 |
Linear momentum is conserved but the velocity of each of the particles in the x-direction is not  = =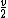 . This would only be true if both particles were moving along the x-axis which is certainly not the case in this problem since they've given you the angle . This would only be true if both particles were moving along the x-axis which is certainly not the case in this problem since they've given you the angle  . .
As the solution stated, by using conservation of linear momentum in the x-direction, you can solve for the velocity of each particle (not the x-component of the velocity)
v'=})
which includes a cos( ) term in the denominator. This cos( ) term in the denominator. This cos( ) term must be less than 1 since ) term must be less than 1 since  must be between 0 and must be between 0 and  . Therefore the velocity (v) must be greater than . Therefore the velocity (v) must be greater than 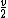
|
Quark
2011-09-26 16:39:36 |
That last line should read "(v') must be greater than 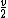 ". ".
|
FutureDrSteve
2011-11-06 14:04:33 |
I'm fairly certain that the x-component of each particle would in fact be v/2. It's the total velocity that is greater than v/2, thanks to the addition of the vertical component of velocity.
|
walczyk
2012-10-07 17:32:57 |
Just thinking about it, and I realize the particles can't deflect at an angle greater than 45 degrees. Since 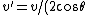) , then we look at the energy: , then we look at the energy: )
|
berri104
2013-10-14 05:26:49 |
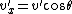
|
|  | Walter
2008-09-02 14:57:08 | Just a trivial matter - you need to apply conservation of momentum vertically to ascertain that because the particles move away at equal angles and have equal masses their velocities must be the same.
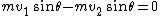
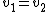
ramparts
2009-10-08 10:57:03 |
No you don't - there's symmetry. There is absolutely no reason for one direction (up or down) to be preferred. Yes, you can do the math to check, but what's the point?
|
|  | Healeyx76
2006-11-02 19:41:40 | another quick way is conservation of energy.
Initial energy is
*m*(V_0)^2)
After you have
*m*(V_f)^2)
You solve 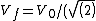)) which is greater than which is greater than 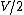
Mindaugas
2007-09-16 01:17:00 |
It is not said that collision is elastic  energy may not be conserved. energy may not be conserved.
|
eoliv001
2010-10-11 16:03:33 |
I agree. There is no mention of this being an elastic collision. You can not assume that.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
