|
GR9277 #44
|
|
|
|
|
Alternate Solutions |
rrfan
2011-11-06 12:45:34 | The Lagrangian is 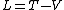 , where , where ) and and 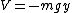 . Only choices (A) and (B) contain . Only choices (A) and (B) contain 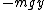 . Of these two, only (A) is possible because . Of these two, only (A) is possible because  must be greater than or equal to must be greater than or equal to 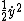 . . |  |
|
|
Comments |
rrfan
2011-11-06 12:45:34 | The Lagrangian is 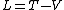 , where , where ) and and 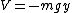 . Only choices (A) and (B) contain . Only choices (A) and (B) contain 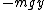 . Of these two, only (A) is possible because . Of these two, only (A) is possible because  must be greater than or equal to must be greater than or equal to 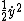 . .
RusFortunat
2015-10-22 16:32:57 |
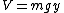
|
|  | Quark
2011-10-26 15:17:39 | This is probably a silly question but, why would one be wrong in choosing choice (E)? I actually picked the right answer (A) on the test but glancing over it again, (E) is also correct in the most general form. Is it not explicit enough? lol
rrfan
2011-11-06 13:14:00 |
the +mgy is wrong.
|
livieratos
2011-11-08 14:41:41 |
also if i remember correctly, since the two coordinates of each other the Lagrangian has to be dependent only on one of them and on its time derivative, not both...
but i could be wrong. guess i should read lagrange and hamilton again :P
|
|  | $null
2009-10-28 16:39:52 | Reposted to  section...(with sexy LaTeX) section...(with sexy LaTeX)
There is a typo in Answer A, it should be 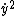 , not , not 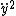 |  | tan
2009-10-14 23:52:17 | There is a typo in Answer A, it should be y dot, not y double dot. |  | mdornfe1
2008-11-06 16:58:28 | This can be done by noticing that potential energy has to be -mgy. A and B are only answers with this property. Second the kinetic energy must always be positive 1-(4ay)^-1 is not always positive. So choice A is the answer.
his dudeness
2010-09-04 13:42:09 |
well done, brah
|
TeamGandalf
2011-04-01 18:12:40 |
The Lagrangian is equal to T-V. Why doesn't the negative from the Potential cancel the negative in the equation?
Why isn't it L = T - (-mgy)= T + mgy?
|
Quark
2011-10-26 15:20:37 |
@TeamGandalf
The lagrangian is L = T - U. You can't have a negative potential energy... U=mgy not (-mgy).
|
|  | Poop Loops
2008-10-12 00:45:40 | So what happens when y = 0, as it inevitably will when the particle comes back down?
segfault
2009-09-04 12:14:26 |
(I realize I'm replying to a 1 year old post--this is for the general public). When y->0, the  term will blow up but term will blow up but 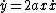 will be zero, so L won't blow up. Perhaps if L was written in terms of will be zero, so L won't blow up. Perhaps if L was written in terms of  it would have a nicer form... it would have a nicer form...
|
|  | etano
2007-06-16 14:12:37 | There is a typo in Answer A, it should be y dot, not y double dot. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
