|
This problem is still being typed. |
Mechanics }Stability of Orbits }Stability of Orbits
The gravitational force suspect to a bit of perturbation is given as 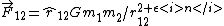 . .
One can narrow down most choices by recalling some basic facts from central force theory:
(A) No mention is made of frictional effects, and thus energy should be conserved.
(B) Angular momentum is always conserved since the net torque is 0 (to wit: the force and moment arm are parallel).
(C) This is just Kepler's Third Law applied to this force. (Recall the following bromide: The square of the period is equal to the cube of the radius---for the inverse square law force. For a perturbed force, the bromide becomes: The square of the period is equal to the 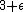 power of the radius.) power of the radius.)
(D) Recall Bertrand's Theorem from Goldstein. Stable non-circular orbits can only occur for the simple harmonic potential and the inverse-square law force. This is of neither form, and thus this choice is FALSE.
(E) Circular orbits exist for basically all potentials. A stationary orbit exists if and only if the following conditions are satisfied:  . Recall that the potential is related to the force by . Recall that the potential is related to the force by 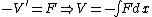 . Use . Use 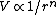 , and recalling the extra term added to the effective potential to be , and recalling the extra term added to the effective potential to be ) , one chunks out the derivatives to get the condition that , one chunks out the derivatives to get the condition that 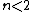 , as a potential exponent, ( , as a potential exponent, (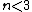 , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For 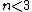 , (the power exponent of the force equation), a stable circular orbit exists. Since , (the power exponent of the force equation), a stable circular orbit exists. Since  is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun. is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun.
|
