|
This problem is still being typed. |
Electromagnetism }Conductors }Conductors
This problem involves applying Coulomb's Law 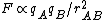 to conductors. The charge travels from conductor to conductor and equilibriates instantaneously due to the requirement that two touching conductors must be at an equipotential. This means that if conductors 1 and 2 touch then their potentials are related by to conductors. The charge travels from conductor to conductor and equilibriates instantaneously due to the requirement that two touching conductors must be at an equipotential. This means that if conductors 1 and 2 touch then their potentials are related by 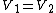 . Because the problem involves spherical conductors, the potential has the form . Because the problem involves spherical conductors, the potential has the form 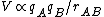 . .
The initial force between the two conductors is 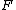 , where , where 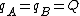 . .
After C is touched to A, the charge becomes 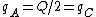 , since each conductor shares the same charge out of a total of , since each conductor shares the same charge out of a total of 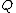 (to wit: each has half of the total charge). (to wit: each has half of the total charge).
When C is touched to B, the charge becomes 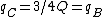 , since each conductor shares the same charge out of a total of , since each conductor shares the same charge out of a total of 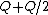 (to wit: (to wit: 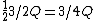 for each conductor). for each conductor).
When C is removed, one calculates the force from Coulomb's law and the final charges on A and B determined above to be,  , as in choice (D). , as in choice (D).
|
