ernest21
2019-08-10 03:09:43 | The problem specifically says y and x are unitless, so does that thinking still hold? drumming games |  |
joshuaprice153
2019-08-08 05:45:19 | I simply stumbled upon your blog and desired to say that I possess really enjoyed browsing your current posts. keep doing your great job and always gain my support. cheers for sharing this beautiful article. commercial cleaning |  |
casseverhart13
2019-07-09 07:03:22 | You\'re really properly informed and extremely intelligent. Orlando Towing Partners Waterford Lakes |  |
JasonHupp
2018-07-30 11:06:29 | Seems like every one must remember the formulas to do the sum and get desired answer.\r\nhttp://www.pumpkin.com |  |
pam d
2011-09-23 19:24:15 | free points! |  |
Dodobird
2010-11-04 18:15:41 | Any solution must involve horizontal and vertical components of force.
Tangents satisfy this requirement.
Because the box weighs 2 kg already we see gravity, the vertical force, will be larger.
Opposite/Adjacent < 1 means that only A satisfies this requirement.
|  |
signminus
2010-08-01 12:15:58 | Not quite. The question asks for the angle,  . As in the posted solution, we have . As in the posted solution, we have
=0.5) . .
To invert this equation, we do
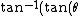)=\text{tan}^{-1}(0.5))
) , ,
answer A.
signminus
2010-08-01 12:16:42 |
Oops, meant that as a reply to rlorek's comment below.
|
|  |
rlorek
2010-07-30 12:32:55 | This was worked out well, but the answers are looking for "arc" functions which are the inverse of normal trig functions.
The inverse of tan(theta)=0.5 is...
arctan(theta)=2.0
Therefor "C" should be the correct answer.
flyboy621
2010-11-09 20:27:00 |
If 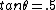 then then 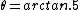 . .
|
|  |
belle
2009-10-11 13:50:56 | This also solvable with simple geometric tactics
tan(theta)=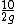
using g=10
tan(theta)=.5
|  |
kostas
2007-01-09 12:42:27 | I see the answers but I cannot find the questions. Where are they? There was a "jump into the question" buton in the old site that I can't see now
yosun
2007-02-22 19:09:03 |
I am in the process of typing up the questions. Currently, only GR8677 is available as graphics file displayed next to the official solution. GR9277 questions will be available shortly, and the rest, eventually.
|
|  |
