|
GR9277 #8
|
|
|
Problem
|
|
\prob{8}
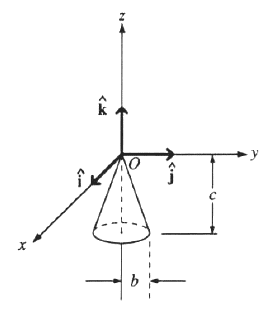
A solid cone hangs from a frictionless pivot at the origin O, as shown above. If 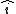 , , 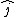 , , 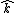 are unit vectors, and a, b, and c are positive constants, which of the following forces are unit vectors, and a, b, and c are positive constants, which of the following forces 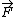 applied to the rim of the cone at a point P results in a torque applied to the rim of the cone at a point P results in a torque  on the cone with a negative component on the cone with a negative component 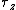 ? ?
-
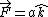 , P is (0,b,-c) , P is (0,b,-c)
-
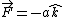 , P is (0,-b,-c) , P is (0,-b,-c)
-
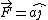 , P is (-b,0,-c) , P is (-b,0,-c)
-
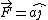 , P is (b,0,-c) , P is (b,0,-c)
-
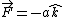 , P is (-b,0,-c) , P is (-b,0,-c)
|
Mechanics }Torque }Torque
The problem wants a negative  component for component for  . Recall that . Recall that 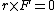 whenever whenever  and and 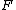 are parallel (or antiparallel). Thus, choices (A), (B), (E) are immediately eliminated. One can work out the cross-product to find that (D) yields a positive are parallel (or antiparallel). Thus, choices (A), (B), (E) are immediately eliminated. One can work out the cross-product to find that (D) yields a positive 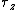 , thus (C) must be it. , thus (C) must be it.
|
|
|
Alternate Solutions |
BerkeleyEric
2010-09-14 15:29:40 | The z-component of the torque (if you write out the cross product) is  . A, B, and E can be immediately thrown out since there is no . A, B, and E can be immediately thrown out since there is no 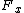 or or  component, and then you can just check to see that C gives the write sign. component, and then you can just check to see that C gives the write sign. |  |
|
|
Comments |
Mall-Saint
2016-10-22 17:08:05 | For a torque with a negative z component, the base of cylinder must be rotating clockwise as viewed from above (by the right hand rule). This can be given by a force applied in the y direction to a point on the far side of the base. Hence (C). |  | hooverbm
2012-10-05 08:21:01 | For those who are getting confused, for some reason I looked at this problem as if the z-direction were out of the page (force of habit). Clearly z is up/down in the plane of the page.
Torque = r X F and when you determine the direction, point your fingers along the direction of "r" and curl through the smallest of the two angles toward "F". Your thumb is the direction of the torque.
You can go through each option fairly quickly. You soon discover that if F is directed along "y", the only way to get a torque that is in the negative "z" is if the "r" has components into the page (-x direction). Thus C. |  | Setareh
2011-11-08 14:15:47 | I really don't understand how you say r and F are parallel in A, B and E...! |  | alimerzairan
2011-10-14 16:31:48 | this is just a test of the right-hand rule.
r = thumb
F = index finger
torque = middle finger
we know that the (A), (B), and (E) can't be true, otherwise the cross product will be 0.
And they want the torque to be in the -z direction. So point your middle finger to the -z direction and you find that the r vector must be in the -i direction. This means a negative x-value which is present in (C). |  | jondiced
2010-11-03 14:15:18 | Remember that 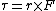 , not , not 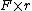 ! Oops. ! Oops. |  | BerkeleyEric
2010-09-14 15:29:40 | The z-component of the torque (if you write out the cross product) is  . A, B, and E can be immediately thrown out since there is no . A, B, and E can be immediately thrown out since there is no 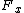 or or  component, and then you can just check to see that C gives the write sign. component, and then you can just check to see that C gives the write sign.
QuantumCat
2014-09-01 12:06:50 |
That's exactly how I solved this problem. I noted that to get 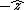 , you have to have a negative , you have to have a negative  crossed with crossed with 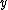 or or  crossed with negative crossed with negative 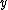 . Since C & D are the only answer choices with a force not in the . Since C & D are the only answer choices with a force not in the 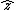 direction, and the force in C & D is the in the direction, and the force in C & D is the in the 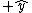 direction, you must have a negative direction, you must have a negative  component, component,  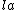 C. C.
Tl;dr: to get 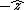 you have to have you have to have 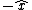   for the given force choices. for the given force choices.
|
QuantumCat
2014-09-01 12:08:42 |
Crap, accidentally put a minus sign in the cross product. It should read: 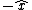  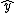
|
|  | yosun
2007-06-01 23:07:02 | test |  | RebeccaJK42
2007-03-22 11:16:55 | Does the R vector point from O to P or P to O?
yosun
2007-06-01 23:06:19 |
R would point from O to P, of course. Recall the right hand rule, and the two axe vectors ( and and  ) that spawn from the same origin. ) that spawn from the same origin.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
