|
GR9277 #9
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
pam d
2011-09-27 22:38:58 | After having seen these practice tests a few times, I can tell anyone that reads this comment that coaxial cables are definitely something to know. |  | none
2008-10-18 14:02:10 | Or more theoretically, the system has axial symmetry, so on a circle centered around the cable, 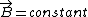 . . 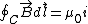 . Enclosed . Enclosed 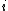 is zero, so is zero, so  must be zero. must be zero. |  | Poop Loops
2008-10-05 13:07:57 | If you don't remember what coaxial cables are for (shielding a current), then you can do it the following way:
The field has to go to Zero at r -> inf (nothing else makes sense), which only leaves choices A (since it's always Zero), and C.
From here you have a good shot at guessing, but if you remember that C is the field for an unshielded wire (Ampere's Law) http://teacher.pas.rochester.edu/phy122/Lecture_Notes/Chapter31/chapter31.html
So A is the only choice left.
ramparts
2009-08-09 16:44:15 |
The other good way to eliminate C is that it's independent of a and b. The only reason to even suspect this answer is non-zero is because a and b are in different places (and presumably because there's more b surface area than a surface area), so it's ridiculous to have an answer that doesn't involve these two quantities.
|
|  | kevglynn
2006-10-14 10:10:11 | If you're like me, you've been through an entire undergraduate physics degree without ever hearing the Magnetic Field referred to as the "magnetic induction." I thought they were talking about electromagnetic induction or something else of which I hadn't heard.
Magnetic Induction is sometimes used for Magnetic field so as not to mix up H and B. I always learned that H was the Auxilliary Field, and B, the Magnetic Field, so be careful if you're like me, and don't slip because of mere semantics.
Furious
2007-10-27 19:08:16 |
Yeah man, I was in the same boat. I was sitting there going like, "Magnetic Induction, what does that have to do with this system." But in the end I remembered that the entire point of coax cables is to keep the E&M inside the wire, so I got this one right.
|
Jeremy
2007-10-29 13:43:31 |
I too was ignorant of the term, and yet, at some time, I must have read what Griffiths has on page 271: "Many authors call 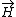 , not , not  , the 'magnetic field.' Then they have to invent a new word for , the 'magnetic field.' Then they have to invent a new word for  : the 'flux density,' or magnetic 'induction' (an absurd choice, since that term already has at least two other meanings in electrodynamics)." Oh well. : the 'flux density,' or magnetic 'induction' (an absurd choice, since that term already has at least two other meanings in electrodynamics)." Oh well.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
