|
GR9277 #82
|
|
|
|
|
Alternate Solutions |
dberger8
2016-08-19 20:19:40 | A lot like jmason86, I arrived at the answer a slightly different way.  . . |  | jmason86
2009-09-03 19:36:44 | I arrived at 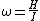 another way. another way.
By analogy: ) and in the rotational system you get and in the rotational system you get ) instead. Since the initial angular velocity was 0, the delta just becomes I instead. Since the initial angular velocity was 0, the delta just becomes I = H. Some simple algebra and bam. = H. Some simple algebra and bam. |  |
|
|
Comments |
dberger8
2016-08-19 20:19:40 | A lot like jmason86, I arrived at the answer a slightly different way.  . . |  | asa1985
2011-10-06 09:43:46 | Torque=dL/dt;
where L is Angular Momentum;
Then H=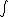 Troque dt Troque dt
H=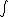 dL dL
H=L
As we know L= Iw
w=L/I |  | kroner
2009-09-26 18:13:21 | We know  will depend on I. The moment of inertia of a linear object like this is going to have a factor of 3 in it somewhere in terms of the mass and length, and there's no way for a factor of 3 to enter into the calculation elsewhere to cancel it out. That leaves choice (D). will depend on I. The moment of inertia of a linear object like this is going to have a factor of 3 in it somewhere in terms of the mass and length, and there's no way for a factor of 3 to enter into the calculation elsewhere to cancel it out. That leaves choice (D). |  | jmason86
2009-09-03 19:36:44 | I arrived at 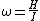 another way. another way.
By analogy: ) and in the rotational system you get and in the rotational system you get ) instead. Since the initial angular velocity was 0, the delta just becomes I instead. Since the initial angular velocity was 0, the delta just becomes I = H. Some simple algebra and bam. = H. Some simple algebra and bam. |  | Anastomosis
2008-04-09 20:51:25 | Although the test book doesn't give the moment of inertia for a plate, it does give it for a rod--if you look at it, a plate is just a thick rod, extended in the z-direction (the direction that has no bearing on the moment of inertia).
Anyway, 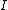 for a rod is for a rod is 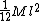 , where , where 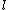 is just equal to is just equal to 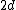 , or , or  in the general case. in the general case.
So, ^2 = \frac{1}{3}Md^2) |  | FA
2007-04-13 00:29:06 | typo alert. there should be no 2 in the denominator of the answer in D) |  | i3taesun
2007-04-11 01:25:54 | Like I=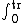 Fdt=delta P, H= Fdt=delta P, H= torque dt=delta L. torque dt=delta L.
Therefore, we should know the changing quantity of angular momentum.
|  | cherianjudy
2006-11-03 16:11:02 | |  | jcain6
2005-11-23 07:00:05 | I think w = at not a/t. This is why w = H/I right?
yosun
2005-11-23 15:02:18 |
jcain6: thanks for the typo-alert; it has been corrected. (while typing up this solution, my pinky was evidently slash-key happy.)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
