|
GR0177 #91
|
|
|
|
|
Alternate Solutions |
Ning Bao
2008-02-01 08:11:02 | Let R, m,h,g=1. Then you just have
1=1/2*8/7+1/2*I*8/7
1=4/7+4/7*I
I=3/4. |  |
|
|
Comments |
redmomatt
2011-10-08 15:23:01 | Did this by process of elimination (not even looking at the PE versus KE).
(A) can't be true, since the cylinder is not of uniform density.
(D) can't be true, since this would only occur if all of the mass were concentrated in a thin ring at a distance 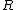 . .
(E) can't be true, since the largest moment would be (D).
We are left with (B) and (C). Because a radial mass distribution that varies as  should be less than something very close to (D), we are left with choice (B). should be less than something very close to (D), we are left with choice (B).
Nezumi
2012-02-09 18:27:24 |
The radial dependence is not given to be linear. I Think (B) or (C) remain until you look at energy.
|
Nezumi
2012-03-06 12:06:24 |
I was looking at the problem again. The elimination you did is the right place to start. Once you have it down to (B) and (C), look at the translational energy.
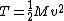
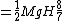
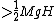
since the translation takes up a little more than half of the original energy of the object, less than half is available for the rotational energy. This implies a smaller moment of inertia, hence choice (B)
|
|  | Ning Bao
2008-02-01 08:11:02 | Let R, m,h,g=1. Then you just have
1=1/2*8/7+1/2*I*8/7
1=4/7+4/7*I
I=3/4.
smokwzbroiplytowej
2008-10-21 11:27:20 |
Nice - sure helps save time! Caveat: you really can't set 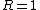 and and 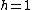 simultaneously, since they are both measures of length. simultaneously, since they are both measures of length.
Here it works rather nicely, because H cancels out as you could tell from the answers.
|
|  | neutrino
2007-10-31 03:28:11 | You can make the calculation more easy by noting that the rotational inertia will look like
 , ,
with  some constant. Now, you just have to solve: some constant. Now, you just have to solve:
)
This might save you some time. Because, 1.7 min..., man, that is not much time.
tommy22222
2019-10-22 14:57:59 |
BRILLIANT!!! I think this is the best and the most make sense alternative solution under this pose.
|
|  | Richard
2007-10-30 18:38:31 | A potentially useless note:
The solution given in (E) is found by NOT accounting for the translational kinetic energy.
|  | Andresito
2006-03-05 00:00:42 | Yosun, there is a typo on your solution. When you express I, the term MV^2 has a factor of 2 implicitly.
Recall the conservation of energy equation, multiply both terms by 2 and the "only" term that has now a factor of 2 is MgH.
The correct expression should have I=(2 MgH - MV^2) (r/v)^2
Yosun, thank you very much for working out the problems. If you are a girl I send you a big kiss :). I obtained the pdf from the yahoo-group. It also has the typo. |  | keflavich
2005-11-10 22:48:10 | You don't need to consider 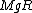 as part of the gravitational potential energy. When the cylinder reaches the bottom of the plane, its center of mass will remain at a distance R above the ground. as part of the gravitational potential energy. When the cylinder reaches the bottom of the plane, its center of mass will remain at a distance R above the ground.
yosun
2005-11-10 22:54:19 |
keflavich: you're right that the center of mass stays at a height of R above the ground at both points. thanks for the correction.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
