|
GR0177 #90
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Normal Modes }Normal Modes
Note that 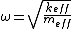 : :
For figure 1, the potential energy is 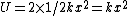 . The kinetic energy is just . The kinetic energy is just 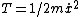 . Thus, . Thus, 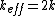 and and 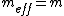 . Thus, . Thus, 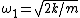 . .
For figure 2, the potential energy is ^2) , since each spring travels only half as far. The kinetic energy is the same as in figure 1. Thus, , since each spring travels only half as far. The kinetic energy is the same as in figure 1. Thus, 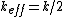 and and 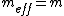 . So, one has, . So, one has, 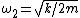
Since 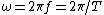 , the period , the period /(2)}=1/2) , as in choice (A). , as in choice (A).
|
|
|
Alternate Solutions |
jax
2005-11-30 18:02:40 | Just remember that capacitors are analogous to springs, so springs and capacitors add in the same way.
Springs in series add like capacitors in series, etc. |  | sf001k
2005-11-10 21:09:52 | springs in series add like resistors in parallel, springs in parallel add like resistors in series. find k effective for system 1 and 2, then get the period. |  |
|
|
Comments |
Masar Smari
2016-07-01 06:47:29 | We can conclude the right solution by simply thinking that as the spring in the second figure travel twice as that in the first figure, the period of oscillation will be twice. Isn\'t it?\r\n\r\n  = =  \r\n \r\n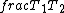 = = 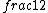 |  | johnVay
2013-10-16 18:50:33 | why isn't this B?   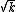  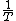
if the effective k's are k & 2k, why aren't the effective periods also have square roots? |  | moonray
2011-04-07 11:36:12 | The period = 2 pi x sqrt m/k(effective) when taking the ratio parallel to series know that series require less force , by inspection this eliminates C D E. Since the k's are all = A would be the best choice if you didnt want to work it out |  | Almno10
2010-11-10 13:38:10 | An earlier question on this GRE tells us spring constant k ===> 1/C (a capacitor).
What I did is made a direct substitution 1/C==> k in the capacitor equations
Ceq(para) = C1 + C2 = 2/k and
Ceq(ser) = 1/(1/c1 +1/c2) = 1/2k.
This game me the answer just fine. These might not be the actual spring constants, but only the coefficients matter (2 and 1/2) since k cancels in the ratio.
Almno10
2010-11-10 19:49:50 |
Furthermore, you can use newton's laws to develop the equations for the eq uivalent k:
Parallel case: when displaced a distance x, the force on the box is kx for each spring, hence F = 2kx
Series Case: A free body diagram would help to see this. When displaced a distance x, each spring compresses x/2. Only one spring touches the box, so the force on the box is F = k(x/2). Thus the effective constant is k/2.
The series case is a reminder that the constant of a spring is a function of its length (more exactly, its number of turns), since doubling its turn number means each portion needs to compress less to achieve a displacement x.
|
|  | joy
2008-11-04 18:40:00 | I'm sorry but I don't understand why springs act like capacitors since k is equivalent to 1/C
Shoudln't it be
In series : 1/C1 + 1/C2 = 1/C  k1 + k2 = k k1 + k2 = k
In parallel C1 + C2 = C  1/k1 + 1/k2 = 1/k 1/k1 + 1/k2 = 1/k
?
Thanks for this awesome site
Dodobird
2010-11-01 11:19:25 |
The analogy between k and 1/C derives from the differential equation, the harmonic oscillator, in which their role is similar. However, this does not imply the extension for calculating effective capacitance and spring constant. These rules are determined independently of the harmonic differential equation. So be careful not to apply the analogy out of context!
|
|  | star
2008-03-01 04:03:29 | just remember that you need mor force for springs in parallel |  | jax
2005-11-30 18:02:40 | Just remember that capacitors are analogous to springs, so springs and capacitors add in the same way.
Springs in series add like capacitors in series, etc.
poljen88
2007-10-27 12:26:12 |
The spring constant k is equivalent to 1/C, so it is the reverse. Springs acting in series are equivalent to capacitors acting in parallel.
|
Richard
2007-10-29 15:26:20 |
My thought exactly...
and if you don't remember the expression for  Yosun quoted, all you have to recall is that Yosun quoted, all you have to recall is that
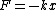 for springs (Hook's law) from which you can use for springs (Hook's law) from which you can use 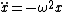
to find the ratio of the periods (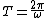 ). ).
|
r10101
2007-11-02 17:27:29 |
jax is correct and poljen88 is not, that is, spring constants add in series/parallel in the same fashion as capacitance. That is, the opposite from the normal for resistors:
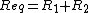 (series) (series)
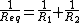 (parallel) (parallel)
So for springs:
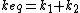 (parallel) (parallel)
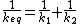 (series) (series)
E.g. http://www.physics.brown.edu/physics/demopages/Demo/waves/demo/3a2020.htm
|
edhopkins
2009-06-28 19:48:12 |
Is it accurate to stake the assumption that both the effective spring constant adds in parallel and the distance traveled is half? It seems like one ought to come from the other. If you ignore the distance traveled you can still arrive at the ratio of periods purely by  = = 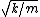 . .
Offhand it seems that by inspection one could assume the distance traveled by the two springs in series is twice that of those in parallel, and intuitively reach the same conclusion.
|
|  | sf001k
2005-11-10 21:09:52 | springs in series add like resistors in parallel, springs in parallel add like resistors in series. find k effective for system 1 and 2, then get the period. |  | sf001k
2005-11-10 21:08:03 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
