|
GR0177 #92
|
|
|
|
|
Alternate Solutions |
uhurulol
2014-10-21 21:55:52 | Process of elimination solution:
Hamiltonian   , a minus in front of the potential , a minus in front of the potential 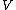 would indicate a Lagrangian. Eliminate (A) (C) and (D). would indicate a Lagrangian. Eliminate (A) (C) and (D).
Spring potential energy and kinetic energy are both proportional to  , not , not 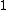 or or  , eliminate (B). , eliminate (B).
All that's left is (E). Hooray. |  |
|
|
Comments |
uhurulol
2014-10-21 21:55:52 | Process of elimination solution:
Hamiltonian   , a minus in front of the potential , a minus in front of the potential 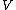 would indicate a Lagrangian. Eliminate (A) (C) and (D). would indicate a Lagrangian. Eliminate (A) (C) and (D).
Spring potential energy and kinetic energy are both proportional to  , not , not 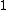 or or  , eliminate (B). , eliminate (B).
All that's left is (E). Hooray. |  | Barney
2012-11-07 09:18:00 | The Test-Takers Solution:
The Hamiltonian is the Energy E of the system - pick choice (E).
(Funny to see that ETS people seem to like little eastereggs. This is not the only case where you can observe such "accidental" matching.) |  | jmason86
2009-07-05 20:04:03 | If you didn't know the potential energy of the spring, you could derive it from Hooke's law.
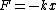
In general, 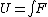 , so , so
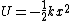
What I don't get is that the negative in Hooke's law doesn't just disappear because you integrate.. so why is potential energy stored in a spring defined to be positive? This would lead to the incorrect answer of (D).
jmg810
2009-07-08 14:19:25 |
If a force is derivable from a position dependent potential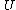 then then 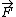 = - = -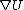 ( (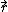 ), and hence ), and hence 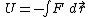 . .
|
jmg810
2009-07-09 09:20:29 |
Typo fix:
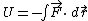
|
jmason86
2009-07-23 17:36:11 |
Thanks!
|
|  | neutrino
2007-10-31 03:34:57 | I don't understand the signs. If the string is ``fully stretched",  , but , but 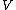 is max. I would guess answer D in this case. is max. I would guess answer D in this case.
What is my error?
hot_dark_matter
2008-05-23 15:00:49 |
If the spring is fully stretched, it doesn't mean that the kinetic energy is zero. Presumably, the directions of 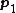 and and 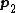 indicate the system can have translational and rotational energy. indicate the system can have translational and rotational energy.
As for the signs, kinetic energy is always positive and so is the potential energy stored by a spring. This eliminates all choices but (B) and (E). Given that there is only one spring, the answer must be (E).
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
