|
GR8677 #76
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mvgnzls
2011-09-26 20:24:02 | energy before = energy after
Mgh=  M M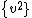 + +  I I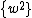 w=v/r w=v/r
Mgh=  M M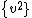 + +  (M (M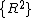 ) )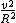
Mgh=  M M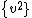 + +  M M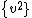
Mgh= M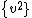
v= 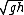
now, L= R x Mv = RMv = RM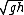
|  | signminus
2010-08-02 14:25:18 | Another POE technique here is to realize that the hoop's angular momentum must depend on its radius (think about a hoop with really huge radius versus one with a tiny radius), so only answers (A) and (B) remain. Of course, something more is needed to get the exact answer, but in a pinch you'll be down to a 50-50 random guess at the worst.
ali8
2011-06-30 09:44:29 |
And if you, in general, are unlucky, like me, then it's really useless.
|
mpdude8
2012-04-19 16:05:57 |
POE is never useless, and if you can narrow it down to a 1 in 2 guess, guessing is a better option than skipping.
|
|  | ben
2006-07-19 16:23:40 | also, units rule out choices (C), (D), and (E). only (A) and (B) have units of angular momentum
jmason86
2009-08-10 20:34:14 |
Totally agreed. I did this.. but they were really mean in giving you a factor of 2 to distinguish the last choice. Damn ETS. Isn't that the first rule of real physics: Factors of 2 don't matter
haha
|
|  | Andresito
2006-03-19 10:39:52 | This solution is confusing. Please specify why the factor of (1/2) disappears when you equate the translational energy with the potential energy.
Thank you
ben
2006-07-20 17:16:01 |
v=R*omega so the translational kinetic energy is equal to the rotational kinetic energy, and that value is (1/2)*M*R^2*omega^2. so when you add 1/2 plus 1/2 you get 1 making the total kinetic energy M*R^2*omega^2. nothing "disappears" here.
|
mvgnzls
2011-09-26 20:23:25 |
energy before = energy after
Mgh=  M M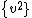 + +  I I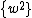 w=v/r w=v/r
Mgh=  M M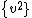 + +  (M (M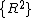 ) )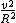
Mgh=  M M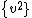 + +  M M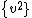
Mgh= M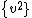
v= 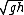
now, L= R x Mv = RMv = RM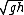
|
danielsw98667
2019-10-21 05:55:38 |
Because the answer is A. semenax review
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
