GREPhysics.NET: GR8677 #60

GR8677 #60

Problem

GREPhysics.NET Official Solution

Mechanics $\Rightarrow$ }Simple Harmonic Motion

Recall $F=-\frac{\partial V}{\partial x}=-2bx$ . Simple harmonic motion has the simple form, $\ddot{x}\propto x$ . Thus $F=m\ddot{x}=-2bx \Rightarrow \ddot{x}=-\omega^2 x$ , where $\omega^2=2b/m$ is the frequency squared. Thus, simple harmonic motion occurs with a frequency determined by both $b$ and $m$ . This is choice (C).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

ernest21
2019-08-23 02:03:37

I enjoyed reading your Solutions together with the answers of others. This is truly a great read for me. brick breaker 2

Reply to this comment

a62
2016-09-20 02:36:59

Easy, but even easier if you look at it this way: a is absolutely meaningless because the zero of potential is arbitrary. So it\'s exactly like the mass-on-a-spring model.

Reply to this comment

Almno10
2010-11-11 23:02:29

Force is the negative gradient of potential energy. The a drops out.

psychonautQQ
2013-09-26 08:41:23

but this is asking for the frequency, how does force and frequency relate?

Reply to this comment

sirius
2008-11-05 22:26:45

A similar solution if you remember $V(x) = \frac{1}{2}m\omega^2x^2$ . The given V(x) has a vertical shift, a, which can be ignored by shifting your zero-point energy. So, 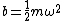$b=\frac{1}{2}m\omega^2$ , solving for $\omega$ makes it depend on b and m.

This is enough, but the problem asks for frequency 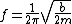$f=\frac{\omega}{2\pi}$ . So $f=\frac{1}{2\pi}\sqrt{\frac{b}{2m}}$ . making f depend on b and m. The answer then is (C).

alemsalem
2010-09-21 06:25:37

i totally agree, to be sure that it doesn't depend on a, just remember that shifting the potential energy by a constant cannot change the motion (classically) so it doesn't affect the frequency.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone