|
GR8677 #62
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
deneb
2018-10-10 04:15:46 | well damn, didn\'t think about E, I solved the equation and saw \"ln\" so I just picked B lol |  | lattes
2008-08-06 13:19:11 | Another way to solve is considering 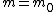 on the choices. None of them gives on the choices. None of them gives  so the answer must be (E) so the answer must be (E)
chrisfizzix
2008-10-03 13:21:18 |
This man speaks the truth. Solving a DEQ no matter how simple is almost always not the way to go about solving an ETS problem. Boundary conditions are definitely the way to go here.
|
shak
2010-07-31 13:03:10 |
in this problem, boundary condition works very good, right:) and also we can always check solution by initial and boundary condition, and eliminate wrong answers
|
|  | Blake7
2007-07-22 20:55:16 | Why would someone attempt a "None of the above" problem on a timed record exam? I see that and think "BYPASS" immediately.
Rune
2007-10-14 22:51:00 |
Because in this case it is very simple as long as you know the  , in which case it takes all of 15 seconds to read and solve. , in which case it takes all of 15 seconds to read and solve.
|
gliese876d
2008-10-17 11:26:40 |
Or because, crazy lunatics like me actually had the eq. for this memorized, so it took 2 seconds to realize the right answer wasn't there :)
|
neon37
2010-11-03 10:18:31 |
None of the above in this was pretty easy to figure but, it was very hard to be quite confident. I must remember use boundary conditions!! It is the way to go for ETS DEQs.
|
llama
2013-10-16 18:47:14 |
Or these days, because you play kerbal space program and have an interest in physics so you know the rocket equation
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
