emergency
2019-09-10 13:27:43 | Before the collision, the COM lies on the middle line, L=mvr where r=0 so L=0 |  |
allenabishek
2017-07-29 10:40:44 | is there a difference between L_trans and L_rot ?? if yes shouldnt both be taken into account ?? why is the standard only taking the translational angular momentum into account ???\r\n
allenabishek
2017-07-29 15:59:05 |
Well you see Allen, L_rot and L_translational are two different things and not the same L_rot = IWo and L_trans = r x p.\r\n\r\nnow for this question we are looking at the total angular momentum which includes both rotational and translational.\r\n \r\nnow by conservation of laws we know \r\n L_total_initial = L_total_final \r\nsince the question asks to find the total final angular momentum it is easier to just find out the total initial angular momentum\r\n\r\nnow L_total_ini = L_rot_ini + L_trans_ini\r\nL_rot = 0.5MR^2W0 ( value of I is found out by looking at the formula sheet)\r\nL_trans = -RMvo ( we get the minus by using the right hand rule)\r\nhere v0 = 0.5RWo so L_trans = -o.5MR^2Wo\r\nthere fore adding them up we get L_tot_ini = 0\r\n\r\nhence the final total angular momentum is zero!!!
|
|  |
allenabishek
2017-07-29 10:35:26 | is there a difference between L_trans and L_rot ?? if yes shouldnt both be taken into account ?? why is the standard only taking the translational angular momentum into account ???\\\\r\\\\n |  |
varsha
2017-02-21 11:20:22 | Either the question is wrong or there is a typo in the answer, it is v0 = 1/2 Rw0 and not v0 = 1/2 R2 w02. |  |
varsha
2017-02-21 11:15:10 | Either the question is wrong or there is a typo in the answer, it is v0 = 1/2 Rw0 and not v0 = 1/2 R2 w02. |  |
arashtavassoli
2016-10-22 00:24:16 | Unfortunately, I don\'t think this answer is correct because the formula 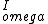 gives the angular momentum about the rotation axis not about point P. gives the angular momentum about the rotation axis not about point P. |  |
socolenco_
2015-11-07 02:09:27 | To really understand this problem we have to imagine that on the edges of the disks there are little slightly-sticky teeth. In this way we can see better that when the first disk hits the edge of the second disk - the first disk continues to rotate counter-clockwise and the second disk initially at rest starts to rotate clockwise. In order for them to cancel their angular momenta due to rotation, the second disk has to rotate counter-clockwise as well. And to cancel also the angular momentum of the second disk due to the transverse motion of the first disk, the second disk has to just rotate a little bit faster. Now because in our problem the disks have no teeth and they stick together at their first touch, the disks have to rotate in opposite directions in order for them to cancel their angular momenta. And this is exactly what is happening - the first disk is rotating counter-clockwise and the second disk will start rotating with the same angular velocity in the opposite direction due to the transverse velocity of the first disk, which means an equal push on each other and a total canceling of their angular momenta. To revise, we have to know that there is an initial angular momentum of the first disk and an opposite angular momentum of the second disk due to the transverse motion of the first disk, and because they stick together this will result in canceling of their angular momenta. As an aside, it would be interesting to calculate the total angular momentum and the angular velocity about the point P in the case of the first disk rotating with the same angular velocity, but clockwise. |  |
gigadan
2013-10-05 17:36:54 | Jesus christ guys, it said clearly, the two disks stick together.
If they stick, would they still spin?
If they don't spin, would there be an angular momentum at point P?
849444209
2013-10-16 10:07:39 |
I think so.You are a genius!!!
|
aziza
2014-08-09 16:28:09 |
Intuitively I would say they do spin about P after sticking, counterclockwise. But I have no clue how to write the equations governing this system. Does anyone have a correct solution?
|
djh101
2014-08-28 22:06:23 |
Yes, they would spin, were v0 not so conveniently chosen.
|
|  |
Joseph Atch
2012-05-20 16:40:45 | For the life of me I can not get the directions from the RHR to work out. I keep getting that both components of angular momentum are in the positive 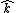 . I curl my fingers along the direction of . I curl my fingers along the direction of  and my thumb points out of the page, and when I try to find the other component I put the first vector pointing from the center of mass of object I to to point P and the second vector pointing along the direction of the velocity of object I, and I get a vector pointing out of the page. I'm probably just overlooking something simple but I can't see it. and my thumb points out of the page, and when I try to find the other component I put the first vector pointing from the center of mass of object I to to point P and the second vector pointing along the direction of the velocity of object I, and I get a vector pointing out of the page. I'm probably just overlooking something simple but I can't see it.
bazzoon
2012-06-08 21:07:20 |
The vector  points from points from 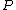 to the center of mass of disk to the center of mass of disk 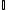 . Thus the cross product of the two points into the page, in the opposite direct to . Thus the cross product of the two points into the page, in the opposite direct to 
|
fermi-on
2012-07-08 15:23:51 |
I find the vector labels the other guy gives a little confusing so I'll give it a try. To use the "finger curling" method of the RHR, the two vectors need to have the same origin. This means that you draw a ray, call it 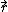 , from P to the center of object I, then extend it past the object. Now, curl your fingers from , from P to the center of object I, then extend it past the object. Now, curl your fingers from 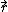 to to  and your thumb should point into the page. and your thumb should point into the page.
|
|  |
k177
2011-11-11 18:25:10 | Right before the collision: 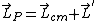
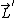 : Angular momentum measured in the center of mass, : Angular momentum measured in the center of mass, 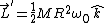 . .
 : Angular momentum of the center of mass, : Angular momentum of the center of mass, 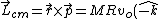) . .
Since  , they have equal magnitudes and opposite directions, and therefore , they have equal magnitudes and opposite directions, and therefore 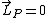 . The answer is A. . The answer is A.
walczyk
2012-10-06 15:10:21 |
Why does v=rw/2 ?!?!?! I only know it as v=rw...
|
gsa
2012-10-12 19:05:48 |
Stated as such in the problem
|
arashtavassoli
2016-10-22 00:32:06 |
From where your starting formula about adding angular momenta comes from. I don\'t think this formula is correct because it suggests that if transition velocity (of cm) is zero, the whole angular momentum about point P is 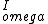 but this is the formula for measuring angular momentum about its axis of rotation which is not equal to angular momentum about P. but this is the formula for measuring angular momentum about its axis of rotation which is not equal to angular momentum about P.
|
|  |
mikey
2011-10-09 17:52:20 | I think it's easiest to look at it at the moment of the collision.
L (for linear velocity) = Iw = I 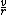
For v, take the top disk's velocity just as it grazes the bottom disk.
L = I 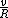 = I = I 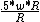 = .5 I * w. = .5 I * w.
Note that it's negative via the right hand rule.
This is the negative of the L (rotational)!
L (rotational) = - L (from linear velocity)
Total L = 0 |  |
mvgnzls
2011-09-27 13:54:04 | I dont know if this is correct but here is how I did it:
Conservation of Momentum so,
angular momentum before = angular momentum after
L = Iw so this has to equal the angular momentum final
which is just
 M M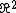 w w |  |
mvgnzls
2011-09-27 13:53:49 | I dont know if this is correct but here is how I did it:
Conservation of Momentum so,
angular momentum before = angular momentum after
L = Iw so this has to equal the angular momentum final
which is just
 M M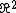 w w |  |
pam d
2011-08-08 20:48:37 | Angular momentum about an ARBITRARY point P is given by the angular momentum of the object's COM w.r.t. P + plus the angular momentum of the object w.r.t. its COM. Plugging in everything gives (A) because the initial angular momentum about P is indeed zero. |  |
lelandr
2011-04-26 13:52:24 | someone had mentioned this earlier, but I thought that I would post it again as a typo:rnrnin the solution: 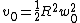 rnrnshould be: rnrnshould be: 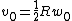 |  |
spunkrat
2010-10-06 18:28:09 | The easy way: Answers A and E are obviously wrong, C and D have the wrong units, leaving B.
jondiced
2010-10-20 17:24:44 |
C and D have the same units as B:
B) ![\frac{1}{2}MR^2\omega_0 = [mass*distance*distance*time^{-1}]](/cgi-bin/mimetex.cgi?\frac{1}{2}MR^2\omega_0 = [mass*distance*distance*time^{-1}] )
C) ![\frac[1}{2}MRv_0 = [mass*distance*distance*time^{-1}]](/cgi-bin/mimetex.cgi? \frac[1}{2}MRv_0 = [mass*distance*distance*time^{-1}])
D) 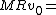 (same as C) (same as C)
|
Crand0r
2010-11-12 14:07:35 |
A is the correct answer.
|
|  |
madanmaun
2010-09-12 09:16:50 | In the first case, there is no rotation of disc I about point P hence there is no angular momentum. Since the angular momentum is conserved it should be zero after collision too.
flyboy621
2010-11-15 20:25:08 |
That's not correct. The angular momentum about point P is given by Yosun's solution and would not be zero in general. It just so happens that in this case the angular momentum from the rotation of disk 1 exactly cancels the angular momentum from the off-center translation of disk 1.
|
|  |
Tatyana
2010-03-08 04:41:12 | Actually rotational angular momentum is determined as 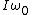 only about rotational axis. We cannot calculate total angular momentum about the point P as only about rotational axis. We cannot calculate total angular momentum about the point P as 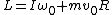 . rnThe line of reasoning leading us to the right answer is folowing. The collision is absolutely nonelastic as it is indicated in the formulation of the problem: "two discs stick together". In nonelastic collisions colliding bodies move as a united body after the collision. It means that relative motion of bodies about the center of mass of the system ceased after the collision. So discs will move translationally as a united body. The rotational part will be lost. Consequently the angular moment about the point P - the center of mass of the system in the moment of the collision - will be equal to zero. A is the right answer. . rnThe line of reasoning leading us to the right answer is folowing. The collision is absolutely nonelastic as it is indicated in the formulation of the problem: "two discs stick together". In nonelastic collisions colliding bodies move as a united body after the collision. It means that relative motion of bodies about the center of mass of the system ceased after the collision. So discs will move translationally as a united body. The rotational part will be lost. Consequently the angular moment about the point P - the center of mass of the system in the moment of the collision - will be equal to zero. A is the right answer.
sina2
2013-10-12 02:19:02 |
I think so.
|
|  |
Tatyana
2010-03-08 04:40:28 | Actually rotational angular momentum is determined as 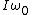 only about rotational axis. We cannot calculate total angular momentum about the point P as only about rotational axis. We cannot calculate total angular momentum about the point P as 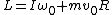 . rnThe line of reasoning leading us to the right answer is folowing. The collision is absolutely nonelastic as it is indicated in the formulation of the problem: "two discs stick together". In nonelastic collisions colliding bodies move as a united body after the collision. It means that relative motion of bodies about the center of mass of the system ceased after the collision. So discs will move translationally as a united body. The rotational part will be lost. Consequently the angular moment about the point P - the center of mass of the system in the moment of the collision - will be equal to zero. A is the right answer. . rnThe line of reasoning leading us to the right answer is folowing. The collision is absolutely nonelastic as it is indicated in the formulation of the problem: "two discs stick together". In nonelastic collisions colliding bodies move as a united body after the collision. It means that relative motion of bodies about the center of mass of the system ceased after the collision. So discs will move translationally as a united body. The rotational part will be lost. Consequently the angular moment about the point P - the center of mass of the system in the moment of the collision - will be equal to zero. A is the right answer. |  |
fred
2008-10-15 21:29:47 | I think the answer sheet is right. At the instant the disks "collide" the moving disk has an angular momentum given by L = r x M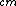 v v , which gives L , which gives L = RMv = RMv = 1/2 MR = 1/2 MR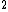 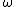  . .
But the disk also has an angular momentum due to it's rotation, which is L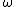 = -1/2MR = -1/2MR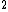 . .
Adding L + L + L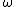 = 0. Since angular moment is conserved, L= 0 before and after the collision at point P. So I think the answer is (A), which explains why (B) = (D). = 0. Since angular moment is conserved, L= 0 before and after the collision at point P. So I think the answer is (A), which explains why (B) = (D).
spunkrat
2010-10-06 18:29:23 |
The easy way: Answers A and E are obviously wrong, C and D have the wrong units, leaving B.
|
spunkrat
2010-10-06 18:29:26 |
The easy way: Answers A and E are obviously wrong, C and D have the wrong units, leaving B.
|
Limerick Jim
2011-10-19 19:18:22 |
C and D have the same units as B as v= r r
the answer sheet is totally correct
|
Setareh
2011-10-29 00:01:02 |
I wonder why some people say that some choices have wrong units. If you notice that all of them has this unit : [L]=[kg][m]^2/[s], you will understand that they all have the correct unit.
|
|  |
Poop Loops
2008-09-23 20:02:33 | My answer sheet says that the answer is A, which makes sense because if one is moving, the other stationary, and they are the same mass, they would each move at half of the speed that Disk I was moving at before the collision.
However, half the angular momentum of Disk 1 gets transfered to Disk 2, but in this case it is spinning in the opposite direction, giving the system zero total angular momentum. Since point P is right in between both disks, it also sees zero angular momentum.
rorytheherb
2008-10-11 13:41:17 |
yeah so what is the correct answer? my answer sheet says (A) zero. It does look like (B) = (D) so how is this a valid question... everyone seems to showing solutions that give (B) = (D) ....
|
Albert
2009-11-02 08:11:48 |
Yes, when I solved it I got the answer (B) as well and it is same as (D), and I don't understand why (A) is supposed to be the right answer since the the bodies stick together after the collision and if so then how could the angular momentum of one cancel that of the other...they are in the same direction for crying out loud!
|
kroner
2009-11-02 17:51:40 |
If you're having trouble visualizing the behavior after the "collision", it will be both disks moving together to the right with no rotation. In that system the top disk contributes a clockwise component while the bottom disk contributes a counterclockwise component. The net angular momentum of the system is zero, just as it is before the "collision".
|
|  |
neutrinosrule
2008-09-21 11:10:48 | I am very confused... I had chosen D for my answer because that's the equation I had gotten to and I saw it in the answer choices... Now that I see that B is the right answer, I am having trouble seeing how B and D are not EXACTLY the same thing... the question DEFINES 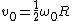 ...and if you just plug in this ...and if you just plug in this 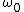 to choice B, you get choice D! What is the flaw in this logic? aren't to choice B, you get choice D! What is the flaw in this logic? aren't 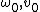 , and R all constants? You yourself had , and R all constants? You yourself had 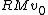 before plugging in... did you just plug in for before plugging in... did you just plug in for 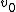 because you knew that the right answer was B or is there some reason why it is wrong to leave the answer like this? Is this possibly a mistake on the part of ETS? because you knew that the right answer was B or is there some reason why it is wrong to leave the answer like this? Is this possibly a mistake on the part of ETS?
spacemanERAU
2009-10-21 17:56:28 |
my answer sheet from ETS says the correct answer is A! i think there is a problem here...anyone know whats up?:
|
kroner
2009-11-02 17:38:31 |
It's true that B and D are the same thing. It's also true that B and D are both the wrong answer so it's not really an issue. The answer is A, as yosun, fred and the answer key all have said.
|
|  |
u0455225
2008-06-14 16:10:17 | It seems to me that answers (B) and (D) are the same thing, by plugging in 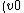 = = _{0}) R into (D). Doesn't this rule out both (B) and (D)? R into (D). Doesn't this rule out both (B) and (D)?
|  |
grayza
2007-09-25 02:27:13 | actually the parrelel axis theorem is needed. It's a trick question look at the arrows in the diagram. The translational angular momentum is in the opposite direction to the rotational angular momentum. The translational moment is  . The translational angular momentum is simply . The translational angular momentum is simply  Therefore the total angular momentum is Therefore the total angular momentum is
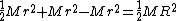 |  |
comorado
2006-10-25 11:40:06 | I think that there is an misprint, you wrote:  , must be , must be 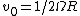 |  |
Jung
2006-10-20 04:02:13 | I have a trouble understanding this solution. From the text, we need to calculate the total angular mementum ABOUT THE POINT P, but I think the angular mementum of rataitional part, IWo, from your solution is not the POINT P, but about its certer. Is it because the moment of inertia I in the text is not about disk 1's center, but about the POINT P? But ETS does not mention about it. How do you think? I love this site! Thank you~
Jung
2006-10-20 04:29:53 |
Is the parallel-axis theorem not needed?
|
sharpstones
2007-03-20 15:01:48 |
I think the problem here is that the terms "rotational/translational angular momentum" are confusing and don't really explain what's going on. In general the angular momentum of a body is 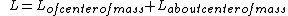 . The angular momentum about the center of mass is Iw, the angular momentum of the center of mass about P is MRv. That's how you get the answer. . The angular momentum about the center of mass is Iw, the angular momentum of the center of mass about P is MRv. That's how you get the answer.
|
Richard
2007-11-01 13:52:28 |
I want to second this comment.
It is absolutely wrong to concern yourself with the "rotational" angular momentum given the wording of the problem. Only consider the MOMENTUM ABOUT P:
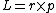
Just before the collision the linear momentum and the radius vector to 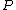 are perpendicular: are perpendicular:
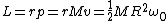
Choice (B).
|
|  |
snimi1
2005-11-05 00:52:25 | Hi, I didn't understand what is the answer eventually. thanks
yosun
2005-11-05 23:20:14 |
Hi snimi1, I've added the explanation for the rotational and translational contributions to the angular momentum. Hope things are clear now.
|
Andresito
2006-03-27 16:20:06 |
I also have trouble understanding this answer in pretty much everything.
|
|  |
rreyes
2005-10-31 12:09:53 | is there something wrong with the equation? L=I , so this is not dimensionally correct? thanks! , so this is not dimensionally correct? thanks!
yosun
2005-11-01 02:25:34 |
yes, there's a rather bad typo here. it's been corrected now.
thanks rreyes!
|
|  |
