|
GR9677 #22
|
|
|
|
|
Alternate Solutions |
mrsparkuling
2016-10-15 19:14:51 | So there is actually NO reason to find the radius of mars. This problem can be done with simple logic. \r\n\r\nWe are told that the golf ball will need to travel 3600 meters in the x direction in the time it drops 2 meters in the y. It should be pretty clear from reason that 3600 meters <<< radius of mars, since mars is a planet which often tend to be larger then a city. So you can now just consider this in a plain with simple newtonian equations. Now there are no forces acting in the x direction so we just have\r\n\r\n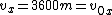 \r\n\r\nNow you can say instantly that this is the answer if you think about it: the velocity is going to be greatly dominiate by the speed in the x direction since x/y = 1800 and x dominates. If you dont believe me:\r\n\r\n \r\n\r\nNow you can say instantly that this is the answer if you think about it: the velocity is going to be greatly dominiate by the speed in the x direction since x/y = 1800 and x dominates. If you dont believe me:\r\n\r\n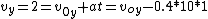 \r\n \r\n \r\nand\r\n \r\nand\r\n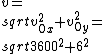 \r\n\r\n \r\n\r\n |  | QuantumCat
2014-09-24 12:18:24 | I believe there is an error in Yosun's solution, as the exact answer can be derived without any difficult calculations.
From Yosun's solution and the geometry (which is the hardest part by far here...) we have:
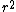 = = 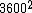 + + ^2)
 = = 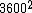   = = 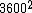 / /
From equating the centripetal force to gravity:
 = = 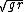
However, since Mars' gravity is one-fourth that of Earth's,
 = = 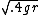 = = 
And putting it all together from our  expression above: expression above:
 = = 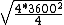 = = 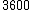 
So,  is seen to be is seen to be  choice C choice C |  | ali8
2011-07-19 00:48:33 | Here's another method to calculate the Radius...
When you go down 2m every 3600m, this means the
tangent of the angle (in radians) is 1/1800. For such
small angles, tan(theta)=theta. Additionally, we can
approximate the circumference of the Mars to be the
sum of all these 3600m segments. But how many such
segments do we have? Well, the sum of the angles
should be 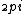 so we have ( so we have (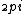 )/(1/1800)= )/(1/1800)=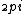 *1800. *1800.
This is the circumference so we have 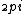 R = R = 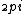
*1800 so R=2*1800*1800.
Now 0.4g*R=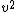 , solve to get the right answer... , solve to get the right answer... |  | Zhi Yong
2009-11-05 04:50:52 | This solution may be confusing as I can't draw diagrams, but I'll try to describe it clearly.
Draw a sector with an arc length of 3600 m, radius r, and angle theta. This sector has an arc and two straight lines. Create a right triangle within this sector by drawing a line from one tip of the arc to the straight line opposite. This right triangle has hypotenus of length r and one side of length r-2.
Notice that cos theta = (r-2)/r = 1 - 2/r, which is approximately 1 - square(theta)/2. Therefore r=4/square(theta).
Arc length s = 3600 = r*theta.
Solving these two equations, r = 1800*1800.
v = sqrt(r*g) = 3600
|  | hamood
2007-04-09 11:49:06 | setting up the problem as this really simplifies it:
In time t , distance x = 3600 m, y = 2 m, a = .4g,
t = 3600/v, and 2 = 1/2*a*t^2....solve the eqs for v. |  |
|
|
Comments |
junksneeze
2016-10-27 18:46:32 | For finding the radius of mars, I found it easiest to think this way: the surface of mars is a circle described by r^2 = x^2 + y^2. Starting at x=0 for example, y = r. We are told that when x = 3600 meters, y = r - 2. So r^2 = 3600^2 + (r - 2)^2. Solve for r. |  | mrsparkuling
2016-10-15 19:14:51 | So there is actually NO reason to find the radius of mars. This problem can be done with simple logic. \r\n\r\nWe are told that the golf ball will need to travel 3600 meters in the x direction in the time it drops 2 meters in the y. It should be pretty clear from reason that 3600 meters <<< radius of mars, since mars is a planet which often tend to be larger then a city. So you can now just consider this in a plain with simple newtonian equations. Now there are no forces acting in the x direction so we just have\r\n\r\n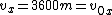 \r\n\r\nNow you can say instantly that this is the answer if you think about it: the velocity is going to be greatly dominiate by the speed in the x direction since x/y = 1800 and x dominates. If you dont believe me:\r\n\r\n \r\n\r\nNow you can say instantly that this is the answer if you think about it: the velocity is going to be greatly dominiate by the speed in the x direction since x/y = 1800 and x dominates. If you dont believe me:\r\n\r\n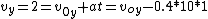 \r\n \r\n \r\nand\r\n \r\nand\r\n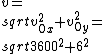 \r\n\r\n \r\n\r\n |  | QuantumCat
2014-09-24 12:18:24 | I believe there is an error in Yosun's solution, as the exact answer can be derived without any difficult calculations.
From Yosun's solution and the geometry (which is the hardest part by far here...) we have:
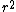 = = 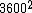 + + ^2)
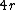 = = 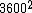   = = 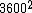 / /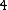
From equating the centripetal force to gravity:
 = = 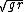
However, since Mars' gravity is one-fourth that of Earth's,
 = = 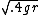 = = 
And putting it all together from our  expression above: expression above:
 = = 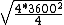 = = 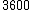 
So,  is seen to be is seen to be  choice C choice C
GradAttemptee
2015-10-19 08:08:18 |
Thanks
|
GradAttemptee
2015-10-19 08:08:47 |
Thanks
|
|  | djh101
2014-09-20 11:14:58 | Well, I can do this problem just fine now, but if I get it on the test, I think I'll be skipping it. |  | Sagan_fan
2013-05-21 14:18:14 | A fun solution for astronomy people:
If you recall the radius of mars is around 1/2 that of Earth, use circular motion to solve. Take g = 4 m/s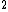 , and by the above reasoning, , and by the above reasoning, 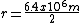
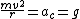 --> v = --> v = 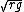 , which is surprisingly close to (C) ~3.6 km/s , which is surprisingly close to (C) ~3.6 km/s
yummyhat
2017-10-28 00:56:57 |
yay
|
|  | hansok49
2011-11-10 21:43:28 | Many Problems I found with this official solution.
1. typo: it's not 2600 but 3600m
2. (3600^2)/2 is not even close to 8E6 since it is 6.48E8
3. how do you randomly get a 2 under that square root when you solve the centripetal acceleration equation?
g on mars is .4g on earth so v should equal 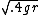 |  | feynman44
2011-11-01 20:41:59 | The final approximation in the official solution, 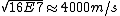 , is far off from the actual value of about , is far off from the actual value of about 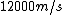 . The solution to the quadratic equation is . The solution to the quadratic equation is 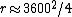 , as opposed to , as opposed to 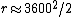 . .
Then we have 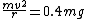 (gravity near the surface of Mars), so (gravity near the surface of Mars), so \frac{3600^2}{4}}=3600m/s) . . |  | ali8
2011-07-19 00:48:33 | Here's another method to calculate the Radius...
When you go down 2m every 3600m, this means the
tangent of the angle (in radians) is 1/1800. For such
small angles, tan(theta)=theta. Additionally, we can
approximate the circumference of the Mars to be the
sum of all these 3600m segments. But how many such
segments do we have? Well, the sum of the angles
should be 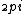 so we have ( so we have (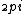 )/(1/1800)= )/(1/1800)=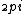 *1800. *1800.
This is the circumference so we have 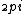 R = R = 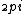
*1800 so R=2*1800*1800.
Now 0.4g*R=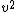 , solve to get the right answer... , solve to get the right answer...
ali8
2011-07-19 00:50:26 |
Clarification:
Actually, we should sum sqrt(3600^2+2^2) but essentially this is 3600....
|
sabrepride
2012-10-10 22:40:15 |
Not certain how you are getting 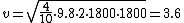 km/s, it appears to be actually km/s, it appears to be actually 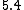 km/s. Otherwise I like your method more. km/s. Otherwise I like your method more.
|
buaasyh
2015-09-30 10:06:02 |
That angle 1/1800 is the tangent chord angle, which is half the corresponding central angle. Thus the central angle corresponding to 3600 meters is 1/900. So the circumference is [2Pi/(1/900)]*3600=2*pi*R. Therefore, R=900*3600=3600^2/4, as derived by QuntumCat above. Then, v=sqrt(gR)= sqrt(4*3600^2/4)=3600. No matter what, this is a novel way to inspect and tackle the problem.
|
|  | Zhi Yong
2009-11-05 04:50:52 | This solution may be confusing as I can't draw diagrams, but I'll try to describe it clearly.
Draw a sector with an arc length of 3600 m, radius r, and angle theta. This sector has an arc and two straight lines. Create a right triangle within this sector by drawing a line from one tip of the arc to the straight line opposite. This right triangle has hypotenus of length r and one side of length r-2.
Notice that cos theta = (r-2)/r = 1 - 2/r, which is approximately 1 - square(theta)/2. Therefore r=4/square(theta).
Arc length s = 3600 = r*theta.
Solving these two equations, r = 1800*1800.
v = sqrt(r*g) = 3600
|  | Albert
2009-10-22 04:42:35 | With almost no calculation required, here is my answer:
For the sake of my lazyness I take g=10m/s^2 as on earth.
For mars, it is 4m/s^2, right?
Flying over Mars, I fall 4 meteres every second, if only I can fly 3600m every second, I gain 2 meters in height, thanks to the curvature of Mars.
Since I am allowed to fall 2 meters every second, I just need to fly with the speed 3600m/s or 3.6km/s and I am good.
Albert
2009-10-22 07:25:22 |
Make it 2 meters, where I say "I fall 4 meters".
|
marc652
2012-09-20 02:38:22 |
I think this is the best solution. Thanks.
|
|  | CaspianXI
2009-03-22 12:06:08 | Yosun gets the right answer the wrong way, as ayabepaula pointed out earlier. IMO, the best solution is from adam. Since he was the first poster, his wonderful solution got buried... do yourself a favor and scroll down to the bottom of the page to see a great solution!
Yosun, I don't mean to criticize you... this is an amazing site! Thank you *so much.* |  | ayabepaula
2008-10-22 10:18:58 | hi !!!!\(^.^)/
Thanks for a wonderful website
1)question:
^{2}+(3600)^{2}=r^{2})
when the
square terms cancel out, and dropping out the 4, one has
 +4+(3600)^{2}=r^{2})
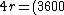^{2})
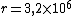
isn't?
or

i didn't understand
|  | Jeremy
2007-10-17 12:14:41 | Wow! The kinematics approach is cool; I hadn't thought of that. Here is yet another approach, this one using similar triangles to find the radius.
Two points on the surface of Mars are connected by the two legs of a right triangle. One leg is 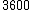 m long, and the other is m long, and the other is  m long. The hypotenuse is a line segment connecting the two points on the surface. The length of the hypotenuse is about m long. The hypotenuse is a line segment connecting the two points on the surface. The length of the hypotenuse is about 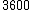 m. The similar triangle is formed with two additional line segments: one connecting the center of Mars and the midpoint of the hypotenuse, and the other connecting one end of the hypotenuse to the center of Mars. The leg resulting from the bisected hypotenuse has a length of about m. The similar triangle is formed with two additional line segments: one connecting the center of Mars and the midpoint of the hypotenuse, and the other connecting one end of the hypotenuse to the center of Mars. The leg resulting from the bisected hypotenuse has a length of about 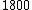 m; the other leg's length is roughly the radius of Mars ( m; the other leg's length is roughly the radius of Mars (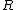 ). Proportionality of the corresponding sides gives ). Proportionality of the corresponding sides gives =(3600 m)/(2 m)=1800) , or , or 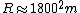 . For the orbit, we have . For the orbit, we have 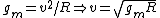 , where , where 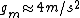 . Therefore, . Therefore, 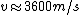 (notice how easy the square root is!). (notice how easy the square root is!). |  | hamood
2007-04-09 11:49:06 | setting up the problem as this really simplifies it:
In time t , distance x = 3600 m, y = 2 m, a = .4g,
t = 3600/v, and 2 = 1/2*a*t^2....solve the eqs for v.
hamood
2007-04-09 11:49:48 |
initially the velocity is only in the x direction with magnitude v.
|
hamood
2007-04-09 11:50:18 |
initially the velocity is only in the x direction with magnitude v.
|
flyboy621
2010-10-23 07:33:23 |
Yes, much simpler this way.
|
natec
2013-09-15 10:11:04 |
this is the way the ETS meant for us to solve the problem.
|
Giubenez
2014-10-15 03:32:08 |
THE SMARTEST!!
|
|  | chri5tina
2006-11-28 03:05:52 | I think the above post should have been labeled as a typo alert, not NEC.
Typo: in the solution, there is an instance where it says "2600" when it should say "3600".
Additionally, in the solution, shouldn't it be that the hypoteneuse is r+2 and the two legs are 3600 and r? I made an attempt to draw a diagram from the current solution, but was unable to.
sirius
2008-11-06 22:38:53 |
It took me a while to figure out the picture, but here's what I've found. If you draw a circle, then on the outside surface draw what is happening. That is draw a tangent line to the circle, until you feel its length represents 3600 m. draw a line perpindicular to it back towards the circle. Draw two lines from the center of the circle: each on to where the two lines intersect the circle. Make one more line that will complete the right triangle Yosun explains.
|
|  | globalphysics
2006-11-01 21:03:27 | I believe the third line should say 3600m not 2600m. Just a detail. :) |  | isak
2006-10-24 11:36:42 | I think there is a mistake here. 2rs=3600^2 so r=3.24E6m. Also v=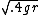 so v=3600m/s. so v=3600m/s.
ps thanks for the excellent resource |  | rreyes
2005-11-27 08:49:50 | In the same spirit as the above comment, for every change in height y, the ball should travel a distance R. We have 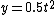 and and 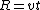 . Dividing, we get . Dividing, we get 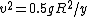 , where , where 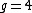 for Mars. After plugging in for y, we get for Mars. After plugging in for y, we get 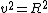 numerically so numerically so 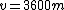 . .
solar39
2009-11-06 09:06:49 |
Yes, one can treat this problem just like a simple trajectory problem. and solve for the speed in the x-direction with the range being 3600 meters and the displacement in the y-direction 2 meters. Just remember to change the g (gravitational acceleration) to 0.4g to get the correct answer!
|
|  | adam
2005-11-09 22:03:19 | This problem easier if you notice the golf ball may fall 2m for every 3600m and still stay at the same height. The time it takes to fall 2m is:
2=1/2(0.4g)t^2
solving for t yields:
t=) approx=1s approx=1s
now the velocity multiplied by the time it takes to fall 2m should equal 3600
vt=3600 v=3600/1 v=3600/1
Baharmajorana
2014-09-14 01:39:00 |
I totaly agree with u . Because this problem is a kinematic problem.
|
|  | Adam D
2005-11-09 21:49:30 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
