|
GR9677 #85
|
|
|
|
|
Alternate Solutions |
Herminso
2009-09-21 12:54:05 | Consider the motion of the end attached to the ring of mass M:
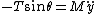 , ,
where T is the tension of the right end of the string applied directly on M making a small  angle with the horizontal, such that angle with the horizontal, such that
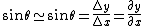 . .
By other hand we know that the string is making a harmonic oscilation of the form 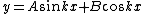 , where , where 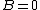 since the left end of the string is fixed, since the left end of the string is fixed, 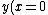=0) . Thus, . Thus,
 and and 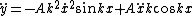 , ,
with 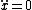 since the wave on the string go at constant velocity given by since the wave on the string go at constant velocity given by 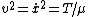 . .
Substituting above,
=M(-Ak^2\frac{T}{\mu}\sin {kx}))   , ,
but 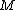 is restricted to move only at is restricted to move only at 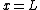 , thus , thus  . . |  |
|
|
Comments |
Yaroslav_Sh
2017-06-28 10:27:48 | Can someone explain me please why do we treat 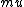 and M as independent parameters?\r\n I would think that if we keep L fixed and increase M by factor of two that would essentially make and M as independent parameters?\r\n I would think that if we keep L fixed and increase M by factor of two that would essentially make 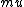 twice larger as well. Yet if it is indeed the case then consideration of large and small limits of M won\'t change twice larger as well. Yet if it is indeed the case then consideration of large and small limits of M won\'t change  at all. at all.
Yaroslav_Sh
2017-06-28 10:32:20 |
Sorry, didn\'t notice that M is mass of the ring, not the string.
|
|  | mpdude8
2012-04-20 18:30:42 | If ETS gives you a hint, use the damn hint.
Eliminate everything except A and B -- those are the only options that can blow up as M --> 0. |  | faith
2010-11-02 00:52:08 | by mathematics, (trigonometry for that matter) and taking ETS hints. the only trigonometry ratio that allows infinity is the tan Teta.
only A and B left.
for M=0, becomes tanTeta= infinity: teta are n pi/2 with n odd integer.
say n=1, 2pi L/lamda=pi/2
L=lamda/4 . sketch this wave length which reveal an unclosed wave (antinode at the end). this implies freedom of movement. hence B is the answer.
Dr. D.R. Dopetec
2011-09-25 12:07:49 |
What about cot(theta)?
|
checkyoself
2011-10-12 13:06:22 |
cot() blows up when it's argument is integer multiples of pi (incl. zero). In the case where M approaches infinity where we know lambda approaches L, the cot() function doesn't work because it will yield infinity when we want zero.
I don't know about the other limit - you have funny values of lambda which I don't understand (help?). Anyway using just the one limit is enough to identify the answer.
|
|  | Herminso
2009-09-21 12:54:05 | Consider the motion of the end attached to the ring of mass M:
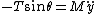 , ,
where T is the tension of the right end of the string applied directly on M making a small  angle with the horizontal, such that angle with the horizontal, such that
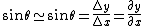 . .
By other hand we know that the string is making a harmonic oscilation of the form 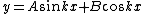 , where , where 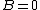 since the left end of the string is fixed, since the left end of the string is fixed, 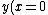=0) . Thus, . Thus,
 and and 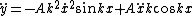 , ,
with 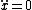 since the wave on the string go at constant velocity given by since the wave on the string go at constant velocity given by 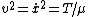 . .
Substituting above,
=M(-Ak^2\frac{T}{\mu}\sin {kx}))   , ,
but 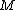 is restricted to move only at is restricted to move only at 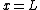 , thus , thus  . .
walczyk
2011-03-30 17:22:11 |
this is awesome. now if there is anyone smart enough to do normal mode oscillation examples, then that would be perfect.
|
hjq1990
2012-10-14 01:33:52 |
Yes, why is ETS bothering contriving 100 questions instead of 10 that require our comprehensive abilities? Is that because in modern time computation is less important than knowing as wide as possible?
|
|  | socks
2008-09-17 10:06:09 | No explicit knowledge of the modes in the  limit is necessary. limit is necessary.
From the 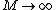 limit we see that there must be modes for limit we see that there must be modes for 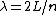 where n is a positive integer. This narrows the choices down to B, C, or D. Choice D is ruled out immediately as we suspect there must be a dependence on the mass of the ring. where n is a positive integer. This narrows the choices down to B, C, or D. Choice D is ruled out immediately as we suspect there must be a dependence on the mass of the ring.
In the  limit, we see that C allows for no modes since the LHS goes to infinity and the RHS is bounded (except for limit, we see that C allows for no modes since the LHS goes to infinity and the RHS is bounded (except for 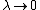 ). The only physical intuition required to obtain choice B is that there must still exist standing modes even for a massless ring. ). The only physical intuition required to obtain choice B is that there must still exist standing modes even for a massless ring. |  | FortranMan
2008-09-03 17:07:15 | for me, the first key was to realize that rapid movement of the string (short wavelength) would require a light ring mass, hence 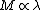 . Then remember . Then remember 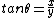 and and 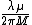 corresponds to components of the wave. corresponds to components of the wave. |  | panos85
2007-10-23 01:32:08 | There is a (minor) inaccuracy in this solution. As M goes to  we have nodes on both sides so every wavelength of the form we have nodes on both sides so every wavelength of the form 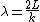 with k=1,2,... is acceptable. (Remember the standing waves.) In a similar way, when M=0, every wavelength of the form: with k=1,2,... is acceptable. (Remember the standing waves.) In a similar way, when M=0, every wavelength of the form: 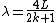 with k=0,1,2,... is acceptable. The answer B is the only one that is satisfied when you plug in these values. with k=0,1,2,... is acceptable. The answer B is the only one that is satisfied when you plug in these values.
QuantumCat
2014-09-23 14:39:10 |
Thanks for clearing this up. I was really confused by the  = = 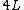 appearance, but this makes perfect sense when I think about it. The analogy I made is that in an open-ended pipe, you get quarter wavelengths, and this situation appears to be the same. appearance, but this makes perfect sense when I think about it. The analogy I made is that in an open-ended pipe, you get quarter wavelengths, and this situation appears to be the same.
|
|  | dumbguy
2007-10-18 21:52:06 | can we still get a better explanation why when M goes to zero lambda=L/4
nontradish
2012-04-19 19:57:40 |
I am sure this will not help dumbguy, but maybe it will help someone else. When M -> 0 picture it as a quarter of a wave. There is one node on the wall and the first antinode on the rod.
|
|  | Mexicana
2007-10-05 14:36:55 | I think there's a mistake in the relation for the fundamental harmonic that you are quoting. Instead this should be 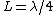 for for  (open end) and (open end) and 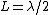 for for 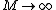 (closed end). In this way the limiting conditions are both satisfied by choice (B) (closed end). In this way the limiting conditions are both satisfied by choice (B)
Lego
2009-01-17 11:50:03 |
Excellent! This is what i had in mind too!
|
|  | cyberdeathreaper
2007-02-04 19:53:47 | Also, can someone explain why the wavelength is 4L when M approaches zero?
hamood
2007-04-11 21:36:40 |
when m approaches zero
node on the left and antinode on the right
L = lambda/4
wavelength = 4L
|
|  | cyberdeathreaper
2007-02-04 19:43:37 | It's unclear to me why the wavelengths of the standing waves have to be of any specified value. For example, when M approaches infinity, the wavelength could be 2L, L, 2L/3, etc...
hamood
2007-04-11 21:39:14 |
when m is very large you have nodes on both ends
|
|  | chri5tina
2006-11-28 06:23:44 | answer A) has a cotangent in it, not a cosine. |  | buddy.epson
2006-10-14 14:18:57 | With M>>mu, lambda=2L, as the antinode is in the center at L/2. That gives the term tan(pi)=0, what you want for the limiting case in (b). |  | alpha
2005-11-07 01:51:52 | Good idea. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
