|
GR9677 #84
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
a
2019-10-09 23:06:25 | Puis, quand MMA est venu autour, je savais que ?a y était, que je pouvais faire les deux en même temps.\r\na http://www.gb-services.net/tobuyen10.asp |  | enterprise
2018-04-07 14:27:53 | There is another way to work this out. Any two-body problem in mechanics can be reduced to one body problem using the concept of reduced mass. So we should expect that the masses should appear as reduced mass in the solution. The only choice in which this happens is D which have K(1/M_1+1/M_2) =K/reduced mass. So , this is the solution.
enterprise
2018-04-07 14:28:52 |
Sorry. It appears in B also , But this doesn\'t involve g/l
|
|  | whereami
2018-04-06 03:32:09 | i think the best way to solve this problem is some sense or knowledge of how the solution of coupled harmonic oscillators look like. Look at m1 and m2. They are on the opposite sides of a spring. This means: you will never see m1 +m2 as a factor in the solution. If you are familiar with some particular solutions of the coupled harmonic oscillator system, you will know this. This mathematical expression is simply un-physical. The only way you see m1+m2 is when you put m2 and m1 together on the same side of a spring. |  | insertphyspun
2011-02-21 11:45:45 | I didn't think to take 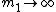 , which I think is the superior way to do this problem. But I did take , which I think is the superior way to do this problem. But I did take 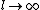 and asked myself what the effective spring constant of the system would be if and asked myself what the effective spring constant of the system would be if 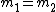 . Consider the following argument: . Consider the following argument:
If 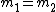 , each mass moves , each mass moves  in the highest normal mode, which is equivalent to one mass moving in the highest normal mode, which is equivalent to one mass moving 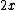 . The potential energy of the system is therefore . The potential energy of the system is therefore k(2x)^2) , giving , giving 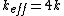 . .
The frequency of oscillation should then be ^{1/2}=(2k/m)^{1/2}) . .
Answer (D) has the correct frequency. |  | gman
2010-11-11 13:45:23 | Take 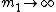 , should get something that depends on , should get something that depends on 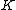 since since 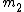 is still attached by the spring. Eliminate A, B and E. is still attached by the spring. Eliminate A, B and E.
Now in that limit, take 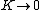 , which is a regular pendulum. Should reduce to , which is a regular pendulum. Should reduce to 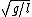 . Eliminate C. . Eliminate C.
Pick D. |  | fjornada
2009-10-18 19:56:52 | take 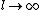 and and 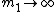 . .
that's just the case of a mass (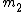 ) oscillating around a fixed point. only (D) has such a limit. ) oscillating around a fixed point. only (D) has such a limit.
his dudeness
2010-07-30 05:30:04 |
Perhaps once you've got it down to choices (D) and (E), you can argue that if you let one of the masses go to infinity so that it's effectively fixed, the normal mode frequency should have some dependence on K, and a larger K will lead to a larger frequency. In (E), the K dependence drops out for this case, so that leaves choice (D).
|
abcdefghijk
2018-04-05 03:13:54 |
well I got down to D and E as well. But instead of taking m to infinity, I took it to zero. In that way D gives an infinitely large frequency. I can\'t make sense out of it. I think a massless m2 simply makes itself disappeared so the system is just a pendulum with a meaningless spring attached it oscillating with f = sqrt (l/g). \r\nThere is something wrong with this reasoning. I hope somebody can help me eventually.\r\n
|
|  | hungrychemist
2007-10-08 22:47:17 | take limit as K-> 0, you should get the lowest normal mode frequency
resinoth
2015-09-18 23:06:29 |
nice.
|
|  | grep
2006-10-27 14:20:32 | If normal mode oscillation isn't your thing, you can use dimensional analysis to eliminate B and E. Then just remember that in general for pendulum systems the frequency decreases when l increases. This leaves only choice D
welshmj
2007-08-02 20:10:18 |
I don't think dimensional analysis can be used here. It certainly does not eliminate B or E.
|
wizang
2009-10-02 00:53:46 |
I checked the units, and they work out on all of the possible answers. Keep in mind that the spring constant is measured in terms of force per unit length. Taking this into consideration, all the answers end up at 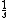
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
