|
GR9677 #92
|
|
|
|
|
Alternate Solutions |
walczyk
2011-04-03 02:05:24 | Hi all, So I didn't want to do it using taylor expansion so I instead used a change in variables after finding the minimum.
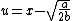
After plugging in and rearranging all the terms you get a pretty attractive potential function, obviously the new minimum is at 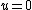 . .
=bu^4+2\sqrt{ab}u^3+2au^2-\frac{a^2}{4b})
Recall  . .
So 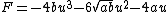 . .
Remember for very small oscillations 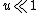 , so higher order terms can be ignored for the ease of this problem. , so higher order terms can be ignored for the ease of this problem.
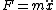 and you undoubtedly know hooke's law, so and you undoubtedly know hooke's law, so 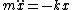 and and 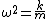 . .
Unfortunately you cannot drop the quartic term after finding the minimum. If you work through the change of variables you find that the quartic term expands to provide a term  and the quadratic term contributes a and the quadratic term contributes a 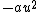 , which is necessary for the right angular frequency. There may be a better answer though, if there is reasoning that there must be a , which is necessary for the right angular frequency. There may be a better answer though, if there is reasoning that there must be a 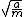 term. That's all folks! term. That's all folks!
|  | munster
2009-10-06 19:13:47 | First of all, you can use dimensional analysis to rule out options (a) and (c). Second of all, we know, without question, that the potential wells caused by the 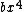 perturbation will be sharper (or deeper, however you like to look at it) than a well described purely by perturbation will be sharper (or deeper, however you like to look at it) than a well described purely by 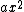 (keep in mind here that the (keep in mind here that the 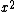 term is NEGATIVE, which means it by itself would not be a potential well, which is why the statement above works). We can see that if the potential were term is NEGATIVE, which means it by itself would not be a potential well, which is why the statement above works). We can see that if the potential were =ax^2) then then  , which rules out (e) because it is too small. (b) doesn't make sense because having a , which rules out (e) because it is too small. (b) doesn't make sense because having a  in the answer would never come up in the proper method (Taylor expansion, etc). This leaves us with (d). in the answer would never come up in the proper method (Taylor expansion, etc). This leaves us with (d). |  | jmason86
2009-09-28 18:28:03 | I did this problem using test taking strategies, although I'm not sure my thoughts were sound:
Since ETS says "for small oscillations" then the 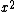 term will dominate. This means that the constant term will dominate. This means that the constant 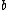 should not be in your answer. Eliminate (A) and (C). should not be in your answer. Eliminate (A) and (C).
 should only become involved if we were asked for period or normal frequency. Eliminate (B). should only become involved if we were asked for period or normal frequency. Eliminate (B).
Getting the frequency is probably going to involve taking a derivative at some point which will bring that 2 down from the 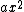 . You'll end up with a 2 in your numerator. Eliminate (E). . You'll end up with a 2 in your numerator. Eliminate (E).
(D) is left. |  |
|
|
Comments |
ETScustomer
2017-10-05 01:52:54 | It\\\\\\\'s such a twist that there\\\\\\\'s no 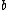 in the answer! Yet, the in the answer! Yet, the 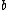 matters ( matters (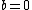 would give a square root of two rather than a square root of four). would give a square root of two rather than a square root of four). |  | Voltsmann
2011-10-12 21:04:53 | I think a lot of people have given basically this solution. But I had some trouble understanding it, so maybe my take on it will help someone. We have the functional form of the potential, V(x). We can find the minima via the usual method: taking the derivative and setting it to zero to find x0 s.t. (dV/dx)(x0)=0 (and checking that the second derivative is positive at x0). Then, since we're interested in small oscillations around xo, we can Taylor expand! We have V(dx)=V(x0)+V'(x0)dx+V''(x0)dx^2/2+O(dx^3), where dx = x-x0. Now we can throw out the first term, because it's a constant, so has no effect on the motion. The second term is zero, because x0 was determined by setting V'(x0) = 0. Then we're left with V(dx) = (1/2)V''(x0)dx^2 = 2a*dx^2. Now the force is F = -dV/dx = -4a*dx. Now we have a Hooke's Law force with k = 4a. The frequency of oscillation is then 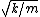 = 2 = 2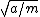 , which is (D). , which is (D). |  | walczyk
2011-04-03 02:05:24 | Hi all, So I didn't want to do it using taylor expansion so I instead used a change in variables after finding the minimum.
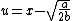
After plugging in and rearranging all the terms you get a pretty attractive potential function, obviously the new minimum is at 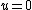 . .
=bu^4+2\sqrt{ab}u^3+2au^2-\frac{a^2}{4b})
Recall  . .
So 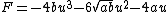 . .
Remember for very small oscillations 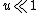 , so higher order terms can be ignored for the ease of this problem. , so higher order terms can be ignored for the ease of this problem.
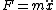 and you undoubtedly know hooke's law, so and you undoubtedly know hooke's law, so 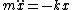 and and 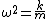 . .
Unfortunately you cannot drop the quartic term after finding the minimum. If you work through the change of variables you find that the quartic term expands to provide a term  and the quadratic term contributes a and the quadratic term contributes a 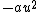 , which is necessary for the right angular frequency. There may be a better answer though, if there is reasoning that there must be a , which is necessary for the right angular frequency. There may be a better answer though, if there is reasoning that there must be a 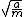 term. That's all folks! term. That's all folks!
|  | munster
2009-10-06 19:13:47 | First of all, you can use dimensional analysis to rule out options (a) and (c). Second of all, we know, without question, that the potential wells caused by the 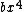 perturbation will be sharper (or deeper, however you like to look at it) than a well described purely by perturbation will be sharper (or deeper, however you like to look at it) than a well described purely by 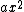 (keep in mind here that the (keep in mind here that the 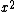 term is NEGATIVE, which means it by itself would not be a potential well, which is why the statement above works). We can see that if the potential were term is NEGATIVE, which means it by itself would not be a potential well, which is why the statement above works). We can see that if the potential were =ax^2) then then  , which rules out (e) because it is too small. (b) doesn't make sense because having a , which rules out (e) because it is too small. (b) doesn't make sense because having a  in the answer would never come up in the proper method (Taylor expansion, etc). This leaves us with (d). in the answer would never come up in the proper method (Taylor expansion, etc). This leaves us with (d).
flyboy621
2010-11-05 23:21:29 |
Well done!
|
|  | jmason86
2009-09-28 18:28:03 | I did this problem using test taking strategies, although I'm not sure my thoughts were sound:
Since ETS says "for small oscillations" then the 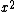 term will dominate. This means that the constant term will dominate. This means that the constant 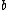 should not be in your answer. Eliminate (A) and (C). should not be in your answer. Eliminate (A) and (C).
 should only become involved if we were asked for period or normal frequency. Eliminate (B). should only become involved if we were asked for period or normal frequency. Eliminate (B).
Getting the frequency is probably going to involve taking a derivative at some point which will bring that 2 down from the 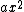 . You'll end up with a 2 in your numerator. Eliminate (E). . You'll end up with a 2 in your numerator. Eliminate (E).
(D) is left. |  | anmuhich
2009-04-02 11:58:57 | I used a really simple way of thinking about this to get the answer in about 20 seconds. Just remember that the potential for a simple harmonic oscillator is 1/2*k*x^2. Since the question says small oscillations around the minima, you can just take the central minimum, which for small oscillations looks a lot like a potential for the SHO, and around which the x^4 term will not contribute hardly. Angular frequency for this SHO is (k/m)^1/2 . But since our original potential is twice that of the potential for the above SHO you know the angular frequency will be greater than (k/m)^1/2 . The extra pi factor for B doesn't really make any sense so the only answer that fits is D.
furlong
2009-08-06 20:39:13 |
how do you know a is greater than 1/2? If a is less than 1/2, then the original potential will be less than 1/2*k*x^2. in other words, did you just assume that a was 1 or am I confused?
|
|  | plapas
2009-04-01 13:31:11 | In this type of exercise, the safest way to solve is the following:
(1) Set dV/dx = 0 and find the roots.
(2) The frequency of small oscillations can be found by the second-derivative term of the taylor expansion, i.e.
(1/2) d/dx(dV/dx) (at min) = (1/2)m ω^2
and through this relation one can find ω.
The method proposed in the solution is good enough,
but one can make a lot of careless errors since the time available for the question is restricted.
mudder
2009-09-28 01:43:22 |
This is good. Solving for ω we see that in general,
Set V'(x_o) = 0
then
ω = (V''(x_0)/m)^(1/2)
Bam! There you go. Simple way of solving SHO problems
|
|  | theodiggers
2007-10-19 19:58:27 | You can also find the minimum, shift the origin of the potential by the minimum so its now centered at zero, then just generate the x^2 term in a Taylor expansion of your shifted potential and get the force from there.
theodiggers
2007-10-19 20:10:42 |
But that triangle expansion method is some sick shit
|
sawtooth
2007-10-30 07:47:35 |
I agree, I prefer finding the minimum 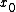 , Taylor expanding around , Taylor expanding around 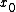 : :
=V(x_0)-V'(x_0)(x-x_0)+V''(x_0)\frac{(x-x_0)^2}{2}+...)
dropping everything except the coefficient of 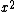 creating something of the form: creating something of the form:
=V(x-x_0)=...+\frac{1}{2}(4\alpha)x^2+... = \frac{1}{2}k x^2)
and we remember that usually 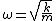 . .
|
sawtooth
2007-10-30 07:52:22 |
Ah, and ofcourse, since 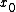 is a minimum is a minimum =0) as we have already used, so no trouble in the expansion, and simirarly, we already have the second derivative (we made sure that it was >0 so its a minimum). as we have already used, so no trouble in the expansion, and simirarly, we already have the second derivative (we made sure that it was >0 so its a minimum).
To be more precise, btw, I should have had
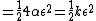
since this is the oscillating quantity... I think!
|
carlosoctavius
2008-08-28 07:48:24 |
How are you getting *4a(x-x0)^2) ? From the Taylor expansion of V(x) we should have ? From the Taylor expansion of V(x) we should have *2a(x-x0)^2) Which leads to the wrong answer :( Which leads to the wrong answer :(
|
|  | TheXDestroyer
2007-09-29 22:42:05 | Can anyone explain how did we move from F(x-x0) to mx''=-4ax
Thanks
antithesis
2007-10-05 07:19:50 |
Plug in the value you found for 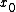 into the line with into the line with 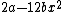 , you get , you get 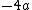
|
|  | cyberdeathreaper
2007-02-18 19:50:59 | I agree - I don't see how this approximation is done. Can someone expand on the steps?
alpha
2007-03-30 22:29:13 |
As mentioned in solution, the approximation is done by using the binomial theorem or Pascal's Triangle, then dropping higher order terms.
(very quick; for 3rd power, it is the 3rd row of Pascal's Triangle with coefficients 1 3 3 1, or ^3 = a^3 + 3a^2b + 3 ab^2 + b^3) ... in the approximation, higher powers of x are dropped out, so we end up with ... in the approximation, higher powers of x are dropped out, so we end up with 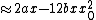 ) )
|
|  | naama99
2006-11-15 16:10:27 | Can someone please elaborate a little on how to do the approcimation? Thanks. |  | alpha
2005-11-07 14:23:08 | kolndom, isn't that what's already there? |  | kolndom
2005-11-07 07:28:01 | Hi, how can a force F=2a*dx leads to small oscillation?
The actual forced experienced by the particle can be given as following:
F=2ax-4bx^3
=2a(L+dx)-4b(L+dx)^3
=2aL(1+dx/L)-4bL^3(1+dx/L)^3
=2aL-4bL^3+2a*dx-4bL^3*3dx/L
=2a*dx-12b*L^2*dx
=2a*dx-12b*(a/2b)*dx
=2a*dx-6a*dx
=-4a*dx
:)
Anastomosis
2008-04-11 13:12:36 |
Mmmm LaTeX:

-4b(L+dx)^3)
-4bL^3(1+dx/L)^3)
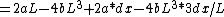
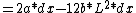
*dx)
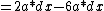
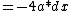
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
