|
GR0177 #75
|
|
|
|
|
Alternate Solutions |
Ning Bao
2008-02-01 07:36:59 | Or...
a_z doesn't change -> Z is the axis -> B or E
The first term in a rotation matrix is cosine, so the angle is +/- 60 degrees-> E. |  |
|
|
Comments |
jw111
2008-11-06 12:38:05 | use vector (1,0,0) -------------- on x-y plane
it become (1/2, -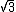 /2, 0 ) ------ on x-y plane /2, 0 ) ------ on x-y plane
and you will conclude the vector rotate 60 degree CW about z-axis
but rember in question, it state this is a transition of components of a vector under different frames
====> (vector not moving)
so the angle should be 60 degree CCW |  | Ning Bao
2008-02-01 07:36:59 | Or...
a_z doesn't change -> Z is the axis -> B or E
The first term in a rotation matrix is cosine, so the angle is +/- 60 degrees-> E. |  | iwf85
2007-10-21 01:31:31 | I think I can clear this up, the question does not ask how the vectors are being rotated, but how the reference frame is being rotated. After all you can think of every rotation as either the vectors being moved in one direction, or the Cartesian plane being rotated in the opposite direction. |  | Mindaugas
2007-09-16 13:10:23 | Vector ) transforms to transforms to ) which means rotation clockwise seeing from the top of z axis. What's wrong in my argument? In the answer rotation is called counterclockwise. which means rotation clockwise seeing from the top of z axis. What's wrong in my argument? In the answer rotation is called counterclockwise.
Blake7
2007-09-21 22:42:39 |
I sympathize with your dilemma. The only 'perspective' that I can offer is that ETS is asking for the
"rotation of the reference frame _S_"
so, (PERHAPS) looking from the S' point-of-view, S will appear to have rotated away 60 deg counterclockwise while looking down into the z axis.
If that ain't it, then I don't get it (right now).
Almost seems like its becoming one of those 'kooky' SR problems : (
|
antithesis
2007-10-01 17:10:33 |
If I'm not mistaken, this is the standard way to look at rotation.
For a coordinate system obeying the right hand rule ( ), a positive rotation will always be counter clockwise. ), a positive rotation will always be counter clockwise.
Maybe it will help looking at the diagram in this page:
http://mathworld.wolfram.com/RotationMatrix.html (This is the view from the positive Z-axis)
|
marten
2007-11-01 17:00:57 |
That totally confused me to
|
his dudeness
2010-09-25 13:27:58 |
Yeah, I had the same problem, which cost me about 45 seconds as I checked and rechecked my math in confusion and despair. I guess ETS is looking for the fact that while a vector is rotated clockwise, the coordinate system itself is rotated counterclockwise. Thank god they at least had the decency not to include "60 deg clockwise about z" among the answer choices, which I wouldn't put past them... To paraphrase my namesake the Dude, "No you're not wrong, ETS -- you're just an asshole!" :-)
|
|  | michealmas
2006-12-31 12:28:01 | if you didn't remember that, you could just tranform a unit vector (1,0,0) and see where it goes.
mhas035
2007-04-07 20:45:24 |
nice
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
