|
GR0177 #76
|
|
|
|
|
Alternate Solutions |
GREview
2009-06-10 17:33:18 | I offer a slight re-phrasing, especially with (D), although I'm not sure about (E):
(A) FALSE: Electrons have less degrees of freedom than free atoms, since electrons are bound to potential wells.
(B) FALSE: My understanding of this is that it would mean that spontaneous heat may be given out by equilibration. Since metals don't just give off heat for no reason, I would say this is not true.
(C) CORRECT ANSWER: A Fermi gas is an ideal gas of electrons, and, given that electrons are fairly free to move around, this would explain why they can be approximated as such a gas in a metal.
(D) FALSE: Free electrons randomly bounce around inside the metal. They do this random motion at near-relativistic speeds. Since a metal can readily conduct (as opposed to a semiconductor), only a light perturbation or change in electric potential across a metal will induce the electrons to move toward the + side of the potential. That velocity is called the drift velocity and, although the electric field from the potential propagates at the speed of light, the drift velocity is surprisingly slow, as Yosun mentioned. However, while ''drifting'' at a slow speed, the electrons also practice their random motion at very high speeds.
(E) : As a hand-waving explanation, what about the idea that regardless of how many sound waves (phonos) are generated by the electron, this has little to do with how fast the electron is moving? Since electrons are free in a metal, the phonons exciting electrons is much less plausible than electrons creating phonons. |  |
|
|
Comments |
whereami
2018-04-07 03:27:19 | I need help. \r\n1. electron has degrees of freedom than atom because they are in potential well. I don\'t understand this logic. Atoms in metals are pretty much fixed while conduction electrons surely seems to have much more freedom than these atoms. \r\n2. thermal equilibrium. if they are in thermal equilibrium, how can electrons have much more kinetic energy than a few KTs ? \r\n3. I don\'t even know what is a fermi gas...I need to read.\r\nI think a good explanation must be much better than what I see now. What I see now is basically favoring certain logic while ignoring other logic without clear explanations. |  | christoski
2011-11-10 20:33:57 | Another explanation for (d): Typical electron densities in metals are n = 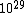 m m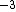 . Using the mass of an electron as . Using the mass of an electron as 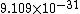 kg, the de Broglie wavelength at room temperature (300 K) is found to be kg, the de Broglie wavelength at room temperature (300 K) is found to be 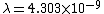 m. The mean interparticle separation is m. The mean interparticle separation is 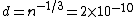 m. This means that m. This means that  >> d and the electrons must be treated quantum mechanically. Another way to think about it is to use the Fermi temperature, >> d and the electrons must be treated quantum mechanically. Another way to think about it is to use the Fermi temperature, 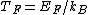 , which must be larger than the actual temperature of the system to be quantum degenerate. Using the same parameters, I obtain , which must be larger than the actual temperature of the system to be quantum degenerate. Using the same parameters, I obtain 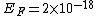 J (or about 12 eV), and J (or about 12 eV), and 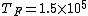 K. This is of course much larger than room temperature. So the electrons have something like 500 times the energy of atoms in the room. K. This is of course much larger than room temperature. So the electrons have something like 500 times the energy of atoms in the room.
christoski
2011-11-10 20:35:30 |
Oops I meant another explanation for (c) the correct answer, not (d).
Ps sorry about the double post
|
|  | christoski
2011-11-10 20:33:40 | Another explanation for (d): Typical electron densities in metals are n = 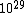 m m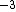 . Using the mass of an electron as . Using the mass of an electron as 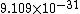 kg, the de Broglie wavelength at room temperature (300 K) is found to be kg, the de Broglie wavelength at room temperature (300 K) is found to be 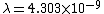 m. The mean interparticle separation is m. The mean interparticle separation is 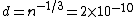 m. This means that m. This means that  >> d and the electrons must be treated quantum mechanically. Another way to think about it is to use the Fermi temperature, >> d and the electrons must be treated quantum mechanically. Another way to think about it is to use the Fermi temperature, 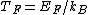 , which must be larger than the actual temperature of the system to be quantum degenerate. Using the same parameters, I obtain , which must be larger than the actual temperature of the system to be quantum degenerate. Using the same parameters, I obtain 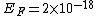 J (or about 12 eV), and J (or about 12 eV), and 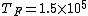 K. This is of course much larger than room temperature. So the electrons have something like 500 times the energy of atoms in the room. K. This is of course much larger than room temperature. So the electrons have something like 500 times the energy of atoms in the room. |  | GREview
2009-06-10 17:33:18 | I offer a slight re-phrasing, especially with (D), although I'm not sure about (E):
(A) FALSE: Electrons have less degrees of freedom than free atoms, since electrons are bound to potential wells.
(B) FALSE: My understanding of this is that it would mean that spontaneous heat may be given out by equilibration. Since metals don't just give off heat for no reason, I would say this is not true.
(C) CORRECT ANSWER: A Fermi gas is an ideal gas of electrons, and, given that electrons are fairly free to move around, this would explain why they can be approximated as such a gas in a metal.
(D) FALSE: Free electrons randomly bounce around inside the metal. They do this random motion at near-relativistic speeds. Since a metal can readily conduct (as opposed to a semiconductor), only a light perturbation or change in electric potential across a metal will induce the electrons to move toward the + side of the potential. That velocity is called the drift velocity and, although the electric field from the potential propagates at the speed of light, the drift velocity is surprisingly slow, as Yosun mentioned. However, while ''drifting'' at a slow speed, the electrons also practice their random motion at very high speeds.
(E) : As a hand-waving explanation, what about the idea that regardless of how many sound waves (phonos) are generated by the electron, this has little to do with how fast the electron is moving? Since electrons are free in a metal, the phonons exciting electrons is much less plausible than electrons creating phonons.
GREview
2009-06-11 13:26:31 |
I realized I made a mistake with (D):
To clarify, CORE electrons (electrons in the valence band) in metals reach near relativistic velocities. CONDUCTION electrons DO NOT, partially due to the shielding of those same core electrons. Core electrons don't make up the "current" in a metal wire. Conduction electrons do, traveling at the above mentioned drift velocity.
Also, phonon-electron interaction is proportional to the temperature. The phonons are the vibrations that occur in a lattice and more of them occur with higher temperature until they become so prevalent that the lattice undergoes a transition to a liquid state.
Feel free to let me know if anything else is wrong.
|
|  | Blake7
2007-09-21 22:53:52 | How about 5 seconds for this one?
"(E) Electron interaction with phonons has nothing to do with their mean kinetic energy."
Huh? That's rather absolute and perhaps even dismissive, Yosun ;)
'I'm from Missouri' (you'll have to type slower -> SHOW ME (please) (Yes, I'm begging and choosing)
Not that I disagree; I just launched into an hour's search for an expression of electrons and phonons to see if KEave was even remotely associated therein.
Richard
2007-10-29 18:08:37 |
And what did you find?
I know that electron-phonon interactions are responsible for the formation of Cooper Pairs which are an integral part of BCS theory.
This explains that electron-phonon interaction allows electron pairs to form at an energy state  than the Fermi energy. than the Fermi energy.
Of course, this is the opposite effect to that explained in the problem, so (E) must be out.
Also, as temperature gets higher, electron-phonon interactions are partly responsible for decreasing conductivity as they interfere with conducting electrons.
Yosun, be careful! You so blithely disregarded (E) while within there is really a lot of important physics.
|
Poop Loops
2008-11-01 20:53:18 |
Sure, but that has to do with more advanced things. We are just looking at electrons flying around in the metal.
A phonon is a a wave in the lattice itself. For this to happen the electron has to smash into an atom. Not only that, but these waves are quantized as well, so you can only have certain momenta and hence certain wavelengths for this phonon/wave.
Then you factor in that an electron has really tiny mass, so it has very little momentum to give an entire atom. When applying a high voltage to really get the electrons going fast, phonons can happen, but when you apply something weak like 5V, that's not a lot of momentum that they are carrying.
|
Poop Loops
2008-11-01 20:54:32 |
Actually, I don't think it's high voltage that would do it, but bombarding the sample with high energy electrons would, that's why you can't always do electron scattering to see the the structure of the lattice. At some point they will just smash into the nucleus and cause a wave/phonon to occur, so you won't get anything useful out of that event.
|
betelguese05
2012-10-10 16:22:32 |
This seemed clear to me. There are just as many phonons in any direction as in any other (isotropic), on average. Thus the average contribution to electron kinetic energy from getting kicks from phonons balances out to zero, so this can't be a reason why conduction electrons have higher KE.
|
|  | grep
2006-10-31 20:37:42 | To prevent the 5 seconds of confusion that I just had for anyone else:
When Yosun says '(B) Why not?' she's not suggesting you save this answer as maybe being correct, but really saying something along the lines of '(B) The electrons SHOULD be in thermal equilibrium with the lattice unless something really weird is going on'
Ge Yang
2010-10-05 21:30:52 |
I was rather confused... Until I saw your comment!
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
