GREPhysics.NET: GR0177 #77

GR0177 #77

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Statistical Mechanics $\Rightarrow$ }Maxwell-Boltzmann Distributions

The Maxwell-Boltzmann distribution is $N\propto g e^{-\epsilon/(kT)}$ , where g is the degeneracy.

Given $\epsilon_a = 0.1+\epsilon_b$ , one finds the ratio of distributions (thus ratio of numbers) to be $e^{-(0.1+\epsilon_b)/kT}/e^{-\epsilon_b/kT}= e^{-0.1/kT}$ .

The problem gives $kT = 0.025$ eV, and thus the above ratio becomes $e^{-.1/.025}=e^{-4}$ , as in choice (E).

Alternate Solutions

Ning Bao
2008-02-01 07:39:44

Quick elimination: higher states are less likely->D or E.

Ratio of given energy to kT mist be important: as Energy of A increases, likelihood in state A decreases ->E.

Reply to this comment

Comments

gbenga 2014-10-18 22:35:18	semi-fast soln: rn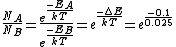 $\frac{N_{A}}{N_{B}}=\frac{e^{\frac{-E_A}{kT}}}{e^{\frac{-E_B}{kT}}}=e^{\frac{-\triangle{E}}{kT}}=e^{\frac{-0.1}{0.025}}$ rnThis power is negative so A,B, & C are eliminated. The denominator is small so D is unlikely. Remaining is E Reply to this comment
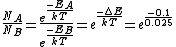
gbenga 2014-10-18 22:32:03	semi-fast soln: $\frac{N_{A}}{N_{B}}=\frac{e^{\frac{-E_A}{kT}}}{e^{\frac{-E_B}{kT}}}=e^{\frac{-\triangle{E}}{kT}}=e^{\frac{-0.1}{0.025}}$ This power is negative so A,B, & C are eliminated. The denominator is small so D is unlikely. Remaining is E Reply to this comment
QuantumCat 2014-09-01 10:39:10	A quick way to solve this problem (knowing that the occupation number depends on the energy) is to say that state B is at zero energy so that the exponential for state B just becomes 1, which is infinitely easier to deal with. Reply to this comment
Ning Bao 2008-02-01 07:39:44	Quick elimination: higher states are less likely->D or E. Ratio of given energy to kT mist be important: as Energy of A increases, likelihood in state A decreases ->E. Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone