|
|
|
| All Solutions of Type: Atomic | | 2 | Click here to jump to the problem! | GR8677 #41
|
Atomic }Binding Energy }Binding Energy
Nickel and Iron are the most tightly bound nuclei, thus have the highest binding energy. Nickel isn't on the list, thus Iron must be the choice.
|
| 3 | Click here to jump to the problem! | GR8677 #48
|
Atomic }Transition }Transition
Transitions go from state one to another state that's completely unique relative to the first state. If both initial and final states have spherically symmetrical wave functions, then they have the same angular momentum. This is forbidden.
|
| 4 | Click here to jump to the problem! | GR8677 #82
|
Atomic }Emission Lines }Emission Lines
(A) The Stern-Gerlach effect has to do with splitting of beams of atoms sent through an inhomogenous magnetic field. Does not have to do with emission spectrum.
(B) The Stark effect has to do with energy shifts via placing atom(s) in an Electric field.
(C) Splitting is often due to electron spin magnetic moments.
(D) The condition is much too rigid.
(E) Splitting of energies means more lines than before. This choice is general enough to be true.
(The effect of energy shifts due to placing an atom in a magnetic field is called the Zeeman Effect, which isn't listed.)
|
| 5 | Click here to jump to the problem! | GR8677 #83
|
Atomic }Spectral Line }Spectral Line
The less dense a gas is, the more precise (thin) its emission lines. So, when one has a dense gas, one expects the spectral lines to be broader---as in choice (C).
|
| 9 | Click here to jump to the problem! | GR8677 #11
|
Atomic }Stern-Gerlach }Stern-Gerlach
Recall the Stern-Gerlach experiment, where (in its original set-up) a beam of neutral silver atoms are sent through an inhomogeneous magnetic field. The beam's split into two---classically, from the Lorentz force, one wouldn't expect anything to happen since all the atoms are neutral, but if one accounts for the Larmor precession, one would expect the beam to be deflected into a smear. Instead, however, the beam deflects into  beams, and thus this supports the idea that electrons are of spin-1/2. (Ag has one unpaired electron in its beams, and thus this supports the idea that electrons are of spin-1/2. (Ag has one unpaired electron in its 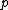 orbital.) orbital.)
With a beam of hydrogen atoms, one should also get a split into two, since 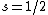 from the electron. from the electron.
|
| 11 | Click here to jump to the problem! | GR8677 #39
|
Atomic }Ionization Potential }Ionization Potential
Atoms with full shells have high ionization potentials---they would hardly want to lose an electron, and thus it would take a great amount of energy to ionize them. Atoms with close-to-full-shells have similarly high potentials, as compared to atoms that are in the middle of the spectrum, take 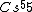 , for example. , for example.
(A) He has a full orbital, and thus its ionization potential must be high.
(B) N has a close-to-full orbital.
(C) O has a close-to-full orbital.
(D) Ar is a nobel gas, and thus its orbital is full.
(E) This is it. Cs has the lowest IP of all (of the above).
|
| 13 | Click here to jump to the problem! | GR8677 #17
|
Atomic }Orbital Config }Orbital Config
First, Check that all choices have superscripts that add to 15. That's apparently so, so one can't easily eliminate choices based on that.
Since the problem has electrons in ground-state, choice (D) and (A) cannot be it--no electrons are promoted from the s to higher orbitals. s has to be filled first.
Choice (E) skips the 3s states completely, so that's out.
One should have an approximate idea of what the periodic table looks like. The transitional (d-state) elements do not occur until after 4s. Even so, the first row of transitional elements is labeled 3d. Since Phosphorous does not have enough electrons to qualify for a 4s or more state, choice (B) must be right.
|
| 16 | Click here to jump to the problem! | GR8677 #30
|
Atomic }Hydrogen Atom }Hydrogen Atom
The hydrogen atom wave-functions all have to do with an exponentially decreasing radial function. Thus, choose choice A. (FYI: Only the spherical harmonic angular parts have trig involved, and thus choice.)
|
| 18 | Click here to jump to the problem! | GR8677 #64
|
Atomic }Radiation Spectra }Radiation Spectra
Choice-by-choice analysis gives...
(A) The word nuclear sounds questionable, as lines are often due to just spin-splitting.
(B) The wavelengths of absorption spectra are often close to that of emissions spectrum (or overlapping). This is true.
(C) Absorption spectra is often used in astrophysics to determine the contents of stars. Even though mere mostly harmless Earthlings have never visited the sun, the absorption spectra of the sun helps determine its component elements.
(D) Same idea as in the previous choice.
(E) A single atom does not have band spectra. So, yes, band-spectra are due to molecules. (To wit: it only has, say, 2s, 3p, etc., states, and not states that are split in-between---molecules have more degrees of freedom, i.e., they can rotate and vibrate, while atoms can't.)
The remaining choice is (A). Take that.
|
| 20 | Click here to jump to the problem! | GR8677 #24
|
Atomic }Bonding }Bonding
Solid Argon is a Nobel gas. It has a full shell of outer electrons, and thus it cannot bond in anything but van der Walls bonding, which isn't really bonding, but more weak like charge-attraction.
One can arrive at this choice by elimination:
(A) Ionic bonding occurs when one atom is a positive ion and the other the compensating negative ion. Since solid Argon isn't an ion, it can't do this.
(B) Covalent bonding occurs when electrons are shared between atoms. This only happens when the atom has unfilled orbitals. (Incidentally, it only occurs when two electrons are of opposite spins due to the Pauli Exclusion Principle. That is, they must have different quantum numbers so that they can both remain stable in a low energy state.)
(C) No partial charge-analysis needed.
(D) Argon isn't a metal.
(E) This is the one that remains.
|
| 22 | Click here to jump to the problem! | GR8677 #58
|
Atomic }Orbitals }Orbitals
Eliminate (E) immediately since the superscripts do not add to 11. Each superscript stands for an electron.
Eliminate (B) because the s orbital can only carry 2 electrons.
Ground state means none of the electrons are promoted, and there are no states with unfilled gaps in them.
Eliminate (A) since it promotes the 2p electron to 3s, leaving a unfilled orbital of lower energy.
Eliminate (D) since it promotes the 3s electron to 3p, leaving an empty orbital of lower energy.
Choice (C) is it.
|
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
