|
GR8677 #41
|
|
|
Problem
|
|
 |
Atomic }Binding Energy }Binding Energy
Nickel and Iron are the most tightly bound nuclei, thus have the highest binding energy. Nickel isn't on the list, thus Iron must be the choice.
|
|
|
Alternate Solutions |
flyboy621
2010-11-14 20:29:23 | All physicists should know that the most common isotope of iron is the most radioactively stable element, hence its abundance in the universe compared to other heavy elements. It's easy to imagine that this stability is due to having a large binding energy per nucleon.
/hindsight |  | Blake7
2007-07-23 17:44:43 | what if Iron wasn't on the list either?
I'm eyeballing a chart (Fig 13-3) in Anderson 'Intro to Modern' (p244) and it shows a curve with a rather flat, totally asymmetric peak of just under about 9MeV per at about A = 60 to 70, so to me that's from about Iron to Gemanium. (how am I to come up with 'the most abundant isotope'?)
Fortunately for us, Iron (C) is 'clearly' the only choice in this band. No doubt there's actually a relation defining this curve. (somewhere)
|  |
|
|
Comments |
ernest21
2019-08-23 02:00:47 | I highly suggest reading through that section. Also, there is some information on Wikipedia: zombie exodus safe haven |  | joshuaprice153
2019-08-09 05:10:30 | I have been just reading through your site it is very well crafted, I am looking around on the net searching for the best way to start this blog thing and your website happens to be extremely professional. tree service Orlando |  | joshuaprice153
2019-08-09 05:08:09 | I have been just reading through your site it is very well crafted, I am looking around on the net searching for the best way to start this blog thing and your website happens to be extremely professional. tree service Orlando |  | 849444209
2013-10-16 06:18:54 | 题目好难啊啊啊啊啊 。没学过啊啊啊啊啊啊 |  | FutureDrSteve
2011-10-30 09:42:46 | I was lucky enough to have just read that atoms with atomic numbers around 30 have the highest binding energy per nucleon. Like kroner said, this was in a discussion about how we add nucleons to small atoms and rip out nucleons from large atoms in order to get energy. Iron's the only one that fits the bill. |  | lelandr
2011-04-24 13:46:08 | I am hoping someone could clarify this for me:
it seems to me that (a) Helium may be the correct answer for this problem...
the problem very clearly states that it is looking for the largest binding energy PER NUCLEON, in which case, Iron (the most stable element) is going to be at a heavy disadvantage to Helium (also a very stable element - on the order of Iron) because of its relatively large atomic number...
the graph at this link also shows this rather well...
http://en.wikipedia.org/wiki/File:Binding_energy_curve_-_common_isotopes.svg
...anyone?
pam d
2011-09-24 10:26:54 |
No, the binding energy curve that everyone is talking about is already binding energy per nucleon. Helium is still on the lower end.
|
|  | flyboy621
2010-11-14 20:29:23 | All physicists should know that the most common isotope of iron is the most radioactively stable element, hence its abundance in the universe compared to other heavy elements. It's easy to imagine that this stability is due to having a large binding energy per nucleon.
/hindsight |  | faith
2010-11-11 22:54:15 | i used the hint..
isotope means the element has same proton number but diff neutron number.
the most abundant isotope would be iron (by logic of star formation) at earth that is.
however, curious doesnt it mean , the more neutron, the lesser the binding energy?since its per nucleon?
pam d
2011-09-24 10:42:08 |
1) Your definition of isotope is too narrow. Every type of element is an isotope. For example, there are 15 isotopes of carbon, including the one where the protons and neutrons occur in equal number.
2) Actually the more neutrons the more nuclear binding energy per nucleon. The two competing forces in holding a nucleus together are the strong force (between protons and neutrons) and the electrostatic force (between protons). The electrostatic force between protons makes the binding energy smaller in magnitude because they repel. Neutrons, on the other hand only contribute to an attractive strong force, making the binding energy higher in magnitude. Think about it and you'll see why it works for "per nucleon" as well.
|
|  | spacemanERAU
2009-10-15 12:21:16 | I remembered from Modern Physics that Iron was the last element on the periodic table that is capable of being fused and guessed that because of this that Iron should be the answer and turns out I was right but Im not sure how to tie the two together. Any suggestions?
kroner
2009-11-01 16:33:37 |
Having the largest binding energy per nucleon is the same as saying its the most stable, or in other words reactions that bring nuclei closer to iron are exothermic. That's why fusing small nuclei up to iron releases energy, and splitting nuclei larger than iron releases energy.
|
|  | evanb
2008-06-19 18:54:31 | A and B can be ruled out, or stars wouldn't frequently create many of the elements we enjoy in abundance on Earth.
D and E can be ruled out, because the binding energy is so low that they decay spontaneously. |  | Blake7
2007-07-23 17:44:43 | what if Iron wasn't on the list either?
I'm eyeballing a chart (Fig 13-3) in Anderson 'Intro to Modern' (p244) and it shows a curve with a rather flat, totally asymmetric peak of just under about 9MeV per at about A = 60 to 70, so to me that's from about Iron to Gemanium. (how am I to come up with 'the most abundant isotope'?)
Fortunately for us, Iron (C) is 'clearly' the only choice in this band. No doubt there's actually a relation defining this curve. (somewhere)
FortranMan
2008-10-26 14:18:56 |
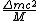 , where , where 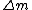 is the difference between the total mass of the element if it was separated into its correct number of protons and neutrons and its atomic mass. Literally, is the difference between the total mass of the element if it was separated into its correct number of protons and neutrons and its atomic mass. Literally,
m_{n} - W)
note M = W*, where the * operator rounds the number to an integer.
|
FortranMan
2008-10-26 14:24:47 |
incomplete post of mine there. 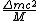 = binding energy per nucleon, = binding energy per nucleon,  =mass of a proton, =mass of a proton, 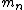 = mass of a neutron, A = atomic number, W=atomic weight, M = atomic mass number (the integer value of W). Thankfully ETS isn't expecting you to be a chemist. = mass of a neutron, A = atomic number, W=atomic weight, M = atomic mass number (the integer value of W). Thankfully ETS isn't expecting you to be a chemist.
|
flyboy621
2010-11-14 20:25:17 |
In hindsight, I guess they wanted us to realize that iron is the most radioactively stable element (hence its abundance compared to other heavy atoms), which probably is considered common knowledge among scientists. Then you just have to make the connection between nuclear binding energy and stability. I doubt they would ask a question like this without iron as one of the answers.
The statement in parentheses is necessary because there are isotopes of iron that are less stable, but those are also less common. The statement is not a hint, but a necessary clarification to ensure that (C) is unambiguously correct. For example, since almost any isotope can exist in theory, you can easily imagine an isotope of iron that is less stable (and therefore has less binding energy per nucleon) than Carbon 14. Allowing all isotopes, any of the answers could be correct.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
