|
GR8677 #31
|
|
|
Problem
|
|
 |
Quantum Mechanics }Photoelectric Effect }Photoelectric Effect
Perhaps one recalls the ``hot phrase" stopping potential. The 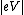 used in the photoelectric equation is essentially the stopping potential (energy). This memory-recall immediately narrows the choices down to just (A) and (C). Now, to find out if the potential is positive or negative. used in the photoelectric equation is essentially the stopping potential (energy). This memory-recall immediately narrows the choices down to just (A) and (C). Now, to find out if the potential is positive or negative.
FYI: The Photoelectric effect equation is basically just conservation of energy. One has 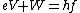 , where , where 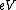 is the kinetic energy of the electron as it accelerates through the medium between the cathode and collector, is the kinetic energy of the electron as it accelerates through the medium between the cathode and collector, 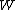 is the energy to free the electron from the metal, and is the energy to free the electron from the metal, and 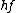 is the energy given by the light source. Essentially, the energy from the photon first frees the electron from a sort of (valence) electron sea it lives in while in the metal, and then the excess energy propels it from cathode to collector in order to keep the current running. The minimum kinetic energy required to get the current going is the stopping potential (energy) is the energy given by the light source. Essentially, the energy from the photon first frees the electron from a sort of (valence) electron sea it lives in while in the metal, and then the excess energy propels it from cathode to collector in order to keep the current running. The minimum kinetic energy required to get the current going is the stopping potential (energy) 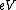 . (According to the fight analogy below, the photon is the one who starts the fight, socking the electron off and away across the currents...) . (According to the fight analogy below, the photon is the one who starts the fight, socking the electron off and away across the currents...)
The electron charge is negative and the potential 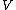 must be a negative quantity in order to make must be a negative quantity in order to make 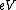 positive overall. positive overall.
(On the lighter side... The Photoelectric effect is also related to the Compton Effect. The effects can be seen as an arena fight. Think WWWF, but with electrons and photons. In PEE, the photon knocks the electron out, while in CE, the electron retaliates! It knocks the photon off course.)
|
|
|
Alternate Solutions |
Jovensky
2013-02-14 01:11:57 | The photon energy is hf and the work function of the photocathode is W. To knock electrons out of the photocathode, the photon energy has to be larger than W. The excess energy will contribute to the kinetic energy of the electron.
If there is zero potential between photocathode and collector, then the electron will just go to collector and generate a current. To counter this, we can generate a force opposing the electron moving direction. This force is given by F=qE. Since this force has points from collector to photocathode and q here is negative. then E has to point from photocathode to collector to make the force points from collector to photocathode. And a useful fact to remember is that electric field points in the direction of decreasing potential. Thus, the collector has to be at a lower potential than photocathode. Since initially the potential is zero, thus, to decrease collector potential, it has to be a negative value.
We can keep on decreasing the potential until at a point, the force is strong enough to repel the electron with the highest kinetic energy and that is the V (stopping potential) in the equation. |  |
|
|
Comments |
fredluis
2019-08-09 04:47:33 | There\'s no such thing as electron-electron annihilation AFAIK. If it existed all the atoms in the universe would turn into nuclei and radiation (losing their electrons). remodeling |  | joshuaprice153
2019-08-09 02:52:11 | So informative things are provided here,I really happy to read this post,I was just imagine about it and you provided me the correct information I really bookmark it,for further reading,So thanks for sharing the information. air duct cleaning Orlando |  | Jovensky
2013-02-14 01:11:57 | The photon energy is hf and the work function of the photocathode is W. To knock electrons out of the photocathode, the photon energy has to be larger than W. The excess energy will contribute to the kinetic energy of the electron.
If there is zero potential between photocathode and collector, then the electron will just go to collector and generate a current. To counter this, we can generate a force opposing the electron moving direction. This force is given by F=qE. Since this force has points from collector to photocathode and q here is negative. then E has to point from photocathode to collector to make the force points from collector to photocathode. And a useful fact to remember is that electric field points in the direction of decreasing potential. Thus, the collector has to be at a lower potential than photocathode. Since initially the potential is zero, thus, to decrease collector potential, it has to be a negative value.
We can keep on decreasing the potential until at a point, the force is strong enough to repel the electron with the highest kinetic energy and that is the V (stopping potential) in the equation. |  | Jovensky
2013-02-14 01:11:28 | The photon energy is hf and the work function of the photocathode is W. To knock electrons out of the photocathode, the photon energy has to be larger than W. The excess energy will contribute to the kinetic energy of the electron.rnrnIf there is zero potential between photocathode and collector, then the electron will just go to collector and generate a current. To counter this, we can generate a force opposing the electron moving direction. This force is given by F=qE. Since this force has points from collector to photocathode and q here is negative. then E has to point from photocathode to collector to make the force points from collector to photocathode. And a useful fact to remember is that electric field points in the direction of decreasing potential. Thus, the collector has to be at a lower potential than photocathode. Since initially the potential is zero, thus, to decrease collector potential, it has to be a negative value. rnrnWe can keep on decreasing the potential until at a point, the force is strong enough to repel the electron with the highest kinetic energy and that is the V (stopping potential) in the equation. |  | spacemanERAU
2009-10-15 09:10:35 | Why does eV have to be positive overall? doesnt the absolute value take care of that?
kroner
2009-10-16 10:43:22 |
There is no "negative value of at which the current stops." Any negative voltage would attract all the free electrons so there would always be a current.
|
his dudeness
2010-08-18 13:12:00 |
kroner, the situation is the exact opposite of what you said. If point B has a negative voltage with respect to point A, then the electric field points from A-->B. This means that positive charges want to drop in voltage and electrons want to go up in voltage. So we need the detector to be at a negative value that's sufficiently high to stop the electron current which arises naturally (even at zero voltage). Tricky stuff!
|
|  | FortranMan
2008-10-19 15:50:26 | Was the question in error in saying hv instead of hf?
FortranMan
2008-10-19 16:11:28 |
my bad, latex fooled me into thinking it was v, and so did the test >:(
|
|  | phys2718
2008-10-16 10:58:57 | Logically, the value of the potential at which the current stops is the same as the value of the potential at which the current starts, depending only on whether you approach it from above or below. This is a stupid question.
justguessing
2009-10-04 06:43:05 |
right, but it says in the question "(...) is initially zero and is then (...) decreased" ... so you know youre coming from the right side. I missed that one, too; because I'm used to read from left to right. Totally agree: Stupid question!
|
mpdude8
2012-04-15 20:57:23 |
I don't think we'll see anything like this on a current GRE.
|
fermi-on
2012-07-07 16:33:48 |
@justguessing
Actually, it says monotonically increased or decreased.
|
cgrman1
2015-04-10 07:35:55 |
They mean the voltage at which there is NO current, not where the current starts or stops in the set-up
|
cgrman1
2015-04-10 08:02:37 |
see Jovensky's solution
|
|  | erc
2005-11-03 14:50:58 | Do you perhaps mean "narrows the answer choices down to (A) or (C)" (i.e. not B)?
Thank you for this exceedingly useful site! Please, please post GR0177 solutions in the next few days!
yosun
2005-11-03 20:07:56 |
erc: thanks for the typo note! It has been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
