|
GR8677 #39
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-09-03 06:24:44 | This problem is really cool.. best carpet cleaner |  | arifmujib
2013-10-13 07:27:40 | The solution is choice A . Because this is a log-log graph . If you take log of ) you'll get you'll get =log(K) - a\omega) which is equivalent of log(Y)=c - mX where c and m are constants . Which is exactly the graph looks like . Solution is A . which is equivalent of log(Y)=c - mX where c and m are constants . Which is exactly the graph looks like . Solution is A . |  | ramparts
2009-10-30 15:26:13 | I *think* this is pretty much Yosun's solutions, but hers is a bit wordy and also poorly-TeXed, so here's my explanation:
A log-log graph is extremely useful because it turns a power law graph (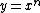 ) into a linear graph ( ) into a linear graph (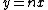 where y and x are the logs of the original y and x). This is a pretty common trick in experimental physics and observational astro. where y and x are the logs of the original y and x). This is a pretty common trick in experimental physics and observational astro.
So you notice the graph looks linear around the relevant point and rule out A in your head (don't even think about it). All you need to do is find the slope. I like the points Yosun used - the point you're given is at y=2 (called 10^2, but it's a log plot) and there's another at y=1 and x=6 (10^6). Now you estimate. It looks like the first point is roughly halfway between 5 and 6 on the x axis, so the slope is about 1/(1/2), or 2. Well, -2, because it's going down. So there you have it - E remains :) |  |
|
|
Comments |
casseverhart13
2019-09-03 06:24:44 | This problem is really cool.. best carpet cleaner |  | joshuaprice153
2019-08-09 04:37:17 | I thought this was going to be some boring old post, but it really compensated for my time. tree service Orlando |  | treebeard
2018-03-05 17:31:01 | On a log-log graph, if a decade of change on the x-axis results in a decade of change on the y-axis, the slope of y=x^b is 1. If a decade change on the x-axis corresponds to a 2 decade change on the y-axis, the slope of y=x^b is 2. In this case, the slope is negative. Had the slope been -1, omega changing from 1e6 to 1e5 (negative change) would have resulted in gain changing from 1e1 to 1e2. Were the slope -2, the same omega change would result in the line intercepting the gain=1e2 line halfway between 1e5 to 1e6, which is ~3e5. It doesn\'t, but it is closer to 3e5 than 1e5 in linear distances, suggesting answer (E). To estimate the slope of a line on a log-log plot, treat the exponents as linear distances on each axis. Even if the log-log plot is not \"square\", the linear relationship holds: a change of 2 decades on the y-axis that corresponds to a 1 decade change on the x-axis indicates a slope of 2. This is all about estimating and ballpark math. |  | OptimusPrime
2017-04-08 00:55:51 | I\'m confused. Choice (E) resembles the function y = 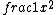 which has positive concavity, not negative like the graph shows. which has positive concavity, not negative like the graph shows. |  | Ashwini
2016-06-19 07:10:13 | In addition to what everyone mentioned, I\'d like to add a 20 second approach too. This\'ll be useful when you\'re running out of time and need a quick way to get this right, in under 20 seconds. We know that that the log-log plot lets us depict a relation of the type \"y=x^m\" into a line \"y=mx+c\". x here is angular velocity. \r\n\r\nIf exponent m is positive, we\'ll have a positive slope and negative a slope if m is negative. Now, this rules out B and C. A is not even of the type \"y=x^m\" (only these type can be represented by a log-log graph as a line), so that goes out too. \r\n\r\nWe\'re left with D and E. You\'ll know by looking at the log-log graph that for m=1, the slope should make equal jumps at equal intervals of x and y. I.e. When x goes from 3*10^5 to 3*10^6, y should jump from 10^2 to 10. But it decreases much faster and goes to 1. Thus, E is the correct answer.\r\n\r\nThose good with basic graphs can just eyeball the graph and conclude that the graph looks too steep to have a +1 or -1 slope. |  | Ashwini
2016-06-19 07:10:12 | In addition to what everyone mentioned, I\'d like to add a 20 second approach too. This\'ll be useful when you\'re running out of time and need a quick way to get this right, in under 20 seconds. We know that that the log-log plot lets us depict a relation of the type \"y=x^m\" into a line \"y=mx+c\". x here is angular velocity. \r\n\r\nIf exponent m is positive, we\'ll have a positive slope and negative a slope if m is negative. Now, this rules out B and C. A is not even of the type \"y=x^m\" (only these type can be represented by a log-log graph as a line), so that goes out too. \r\n\r\nWe\'re left with D and E. You\'ll know by looking at the log-log graph that for m=1, the slope should make equal jumps at equal intervals of x and y. I.e. When x goes from 3*10^5 to 3*10^6, y should jump from 10^2 to 10. But it decreases much faster and goes to 1. Thus, E is the correct answer.\r\n\r\nThose good with basic graphs can just eyeball the graph and conclude that the graph looks too steep to have a +1 or -1 slope. |  | Ashwini
2016-06-19 07:10:11 | In addition to what everyone mentioned, I\'d like to add a 20 second approach too. This\'ll be useful when you\'re running out of time and need a quick way to get this right, in under 20 seconds. We know that that the log-log plot lets us depict a relation of the type \"y=x^m\" into a line \"y=mx+c\". x here is angular velocity. \r\n\r\nIf exponent m is positive, we\'ll have a positive slope and negative a slope if m is negative. Now, this rules out B and C. A is not even of the type \"y=x^m\" (only these type can be represented by a log-log graph as a line), so that goes out too. \r\n\r\nWe\'re left with D and E. You\'ll know by looking at the log-log graph that for m=1, the slope should make equal jumps at equal intervals of x and y. I.e. When x goes from 3*10^5 to 3*10^6, y should jump from 10^2 to 10. But it decreases much faster and goes to 1. Thus, E is the correct answer.\r\n\r\nThose good with basic graphs can just eyeball the graph and conclude that the graph looks too steep to have a +1 or -1 slope. |  | QuantumCat
2014-08-30 11:16:17 | According to the answer key at the back of the test, the answer is E. |  | tweetie_bird
2014-02-08 19:05:45 | I think it is important to spell out that last line.
10 = (1/3) ^n
So you are basically saying 1/3 raised to what power gives you 10.
If you raise 1/3 to the -2 power you get 9, which is closest to 10.
So the answer is -2 for the exponent. |  | arifmujib
2013-10-13 07:27:40 | The solution is choice A . Because this is a log-log graph . If you take log of ) you'll get you'll get =log(K) - a\omega) which is equivalent of log(Y)=c - mX where c and m are constants . Which is exactly the graph looks like . Solution is A . which is equivalent of log(Y)=c - mX where c and m are constants . Which is exactly the graph looks like . Solution is A .
llama
2013-10-16 19:31:36 |
Nope. Disagreeing with the answers given on the exam papers is usually a bad idea, and definitely in this case. Exponential relations come from log-linear graphs.
|
camarasi
2017-10-25 14:13:14 |
But the X-axis is a log too and looks like a straight line, so it must be a log of X, not just X.
|
|  | anum
2010-11-08 12:59:14 | what i did was simply look at the graph at the given region near 3 x10^6 and it looked nothing like exponential decay couldn't have been a linear decay because the slope is not straight left was the 1/w^2 decay |  | testtest
2010-10-08 16:31:44 | More detailed explanation on finding slope of log-log plot: http://en.wikipedia.org/wiki/Logarithmic_scale#Slope_of_a_log-log_plot |  | ramparts
2009-10-30 15:26:13 | I *think* this is pretty much Yosun's solutions, but hers is a bit wordy and also poorly-TeXed, so here's my explanation:
A log-log graph is extremely useful because it turns a power law graph (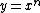 ) into a linear graph ( ) into a linear graph (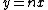 where y and x are the logs of the original y and x). This is a pretty common trick in experimental physics and observational astro. where y and x are the logs of the original y and x). This is a pretty common trick in experimental physics and observational astro.
So you notice the graph looks linear around the relevant point and rule out A in your head (don't even think about it). All you need to do is find the slope. I like the points Yosun used - the point you're given is at y=2 (called 10^2, but it's a log plot) and there's another at y=1 and x=6 (10^6). Now you estimate. It looks like the first point is roughly halfway between 5 and 6 on the x axis, so the slope is about 1/(1/2), or 2. Well, -2, because it's going down. So there you have it - E remains :)
Albert
2009-11-01 04:29:00 |
ramparts wrote "I *think* this is pretty much Yosun's solutions, but hers is a bit wordy and also poorly-TeXed, so here's my explanation"
That's pure insult! And fella, how is your solution any better than hers? I didn't get anything new at all from you. Plus, yours is not even properly formatted and don't even get me started on 'poorly-TeXed'.
|
Prologue
2009-11-06 17:09:09 |
Although your solution could have done without the veiled insult it is definitely better because it gives background. I think it is important to realize that the person coming to this page is not sure of what the answer is, thus you need to spell it out for them, so that they are sure they understand it once they leave. After doing hundreds of solutions I am sure yosun gets tired and sees the easy way to do things and then just does them, but that is not the situation for the person visiting the site. They (I) need hand holding. So, give a complete background on the problem and everyone is happy.
|
neon37
2010-11-01 12:08:45 |
Yea plus you can eliminate B and C cuz the slope is clearly negative. Good explanations. Makes it clear why Yosun chose those points.
|
flyboy621
2010-11-14 20:05:04 |
First of all, we all agree Yosun deserves major credit for putting this site together. That said, let's not flame someone for trying to clarify Yosun's solution. I personally find ramparts's solution helpful, and I don't think it was that insulting.
|
|  | PhyAnnie
2008-11-04 22:53:23 | Sorry, but you all seem wrong here. The graph itself is a log-log graph, i.e. it's ln(w).vs.ln(Gain). (you can easily tell by the non-uniform scalm of x-y axis). Having that in mind, we get : ln(Gain)=-2*ln(w), such the answer.
Cheers~
wittensdog
2009-07-25 19:42:57 |
I agree, but I also added in a non-zero y-intercept in the relation between the two logarithms. When you exponentiate both sides to find the Gain as a function of frequency, this is where the factor of K out front comes from. I found the value of negative two for the slope relating the two logarithms merely by eye-balling the graph. It's clearly negative, and it's too steep to be negative one. Also, I think A is a trap, because this plot clearly involves base 10 logarithms, not natural logarithms, so e shouldn't factor into the answer.
|
|  | sonnb
2008-06-07 11:16:48 | In your solution, I'm sure you meant ^n) instead of instead of ^n) . Of course, the difference is insignificant. . Of course, the difference is insignificant. |  | Furious
2007-08-31 09:26:41 | Hey, I'm probably confused. But I eliminated all choices but A by looking at the limiting behavior as  goes to zero. All choices including E, either go to zero or infinity as goes to zero. All choices including E, either go to zero or infinity as  goes to zero, while A tapers out to a constant value. And I'm not sure, but that decay at the end doesn't look too bad for an exponential, on a log-log plot, does it? goes to zero, while A tapers out to a constant value. And I'm not sure, but that decay at the end doesn't look too bad for an exponential, on a log-log plot, does it?
D8less
2007-10-04 19:06:15 |
Yes, you are confused. The question just asks about how the function behaves at just one point. You are looking at the whole function but you should be thinking locally.
|
Richard
2007-11-02 18:22:34 |
I did the same thing...
I don't understand. How can it be anything but (A)?
...Unless of course, it blows up where you can't see it.
Then again, it just asks for which is most accurate near 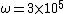 . .
|
naseermk
2008-09-22 17:02:08 |
If you apply the limiting condition of w approaching infinity, only D /E results in a gain that approaches zero as we see in the plot.
|
naseermk
2008-09-22 17:02:32 |
If you apply the limiting condition of w approaching infinity, only D /E results in a gain that approaches zero as we see in the plot.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
