|
GR8677 #26
|
|
|
|
|
Alternate Solutions |
Limerick Jim
2011-10-14 15:34:42 | way simpler guys: GRE means speed
Use: E=hf=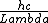
x-rays are around 10^-10 (x-rays are on the order of atoms, thats why we use them for x-ray diffraction of crystals), You should know the speed of light or you should kill yourself, and h in eVs is quoted in the constants. plug it in to get 12 x 10^3 which aprox equals 10,000 eV
BillNyeTheRussianSpy
2018-05-20 03:49:57 |
I come for the physics, but stay for the suicide.
|
|  | barefoot0
2006-11-14 11:17:02 | I dont know if this exactly correct but I did the following.
I know 2.5eV gives ~ 500nm (This is just an easy thing to remember and quite usefull).
X rays are about .1 nm and E is inversly proportional to Lambda so
2.5eV*500nm/.1nm ~ 10,000 eV
Someone let me know if and why this method is wrong. |  |
|
|
Comments |
harmonxjim33
2019-10-01 14:06:28 | Those guidelines additionally worked to become a good way to recognize that other people online have the identical fervor like mine to grasp great deal more around this condition. mobile legends new hero |  | fredluis
2019-08-09 04:29:11 | Not a rigorous answer, but in a multiple choice environment, it really doesn\'t matter. carpet cleaners |  | joshuaprice153
2019-08-09 02:32:00 | I’ve desired to write something similar to this on my webpage and this has given me an idea. Cheers. security guard Jacksonville |  | physics_guy
2018-08-08 15:16:41 | The problem is just asking for the binding energy of one of the n=1 electrons in nickel, since if this electron is removed via bombardment of fast electrons, an n=2 electron will fall into its place, releasing a photon in the x-ray range. This phenomenon is known as the Auger effect, and it is used in Auger Electron Spectroscopy (AES). The photon released during this transition is known as the K-alpha line in x-ray spectroscopy. This transition was famously studied by Moseley to provide strong evidence that atomic number is identical to nuclear charge. While it is perfectly reasonable to use Moseley\'s formula for the transition from n=2 to n=1, it is not really correct since that would give you the energy of the released photon. What we really want is the binding energy of one of the two n=1 electrons, 13.6ev * Z^2. While it is also reasonable to account for the screening of nuclear charge by the other n=1 electron, the correct way to account for screening by electrons in the same orbital is to subtract 1/2 from Z, not 1. Fortunately, most of the solutions above all work out to the same order of magnitude. However, the setting of initial n to infinity shows a misunderstanding of the role of the bombarding electrons in the Auger effect, which do not undergo transitions themselves, but merely knock out core electrons with energy less than or equal to the kinetic energy of the bombarding electrons, leaving holes to be filled by higher-orbital electrons. The K-series corresponds to the removal of an n=1 electron, causing a transition from n=2 to n=1 to fill the hole. This is analogous to the Lyman-alpha transition in hydrogen. |  | Limerick Jim
2011-10-14 15:34:42 | way simpler guys: GRE means speed
Use: E=hf=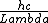
x-rays are around 10^-10 (x-rays are on the order of atoms, thats why we use them for x-ray diffraction of crystals), You should know the speed of light or you should kill yourself, and h in eVs is quoted in the constants. plug it in to get 12 x 10^3 which aprox equals 10,000 eV
ryanjsfx
2014-10-20 11:47:24 |
1) I messed up this problem by doing it that way but taking X-ray wavelength to be 1e-11 meters (which is still X-rays) and it turned out using that gets (E) so I think that approach assumes more than is given.
2) If you just remember E is approximately  where Z is the number of protons [Bohr energy approximation] then rounding 13.6 to 10 and 28 to 30 yields E = (10)(30)(30) = 1e4 much quicker than doing the (admittedly still rather simple) multiplication of h c and one over lambda. where Z is the number of protons [Bohr energy approximation] then rounding 13.6 to 10 and 28 to 30 yields E = (10)(30)(30) = 1e4 much quicker than doing the (admittedly still rather simple) multiplication of h c and one over lambda.
|
DownWithETS
2016-10-30 14:36:23 |
I used this method also, but it doesn\\\\\\\'t really work. X rays range from wavelength=10 nm-.1 nm. If you assume the high-end energy limit of .1 nm, then it works, but using either 1 or 10 nm values gets us a different order of magnitude, which are both possible choices. Is there some reason you know to choose the highest energy x-rays?
|
BillNyeTheRussianSpy
2018-05-20 03:49:57 |
I come for the physics, but stay for the suicide.
|
|  | engageengage
2009-01-17 15:02:26 | Im not sure why people are talking about atomic transitions. If you want to produce x-rays in the K series, you must knock out the first electron. This will then cause more energetic electrons to transition into the newly free state, emitting x-rays along the way. Therefore, you wind up with the same equation that yosun has, where you take screening into account:
13.6eV ( Z-1)^2
wittensdog
2009-07-25 16:56:30 |
I agree, the only thing that matters for producing K series x rays is that you have a hole for other electrons to drop back into in the n = 1 shell. So the only thing your electron needs to do is pop out an n=1 electron. The only formula I ever made reference to was the hydrogenic atom approximation to the Bohr energy formula, E = - 13.6 * Z^2 / n^2. In this case n = 1 and Z = 28. There is also the issue of screening. I do not recall how much screening one of the n = 1 shell electrons should provide for the other. In chapter 7 of Griffiths' QM textbook you can see that for Helium, the screening results in around 1.69 as opposed to 2. I'm not sure how much all of the electrons in the outer shells affect that, but it hardly matters for this problem, since using 27 or 28 results in either 9,914.4 or 10,662.4, respectively, all of which are certainly much closer to 10,000 than anything else. My preferred method for the approximation is to write everything in scientific notation and pull apart the factors, so you end up with 1.36 * (2.8) ^ 2 * 1,000. With this, it's obvious that 27 vs. 28 hardly makes a difference, and the factor out front is roughly 10. If the problem involved the specific energies of the x rays emitted, then you would need the Rydberg formula, but this is not the case here.
|
|  | a19grey2
2008-11-03 20:29:42 | Uh, am I the only person who calculates the value using 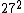 and and 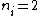 , , 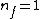 and gets only ~7,400. and gets only ~7,400.
doing this on a test , I'd still guess the right answer, but this seems to far off for this to be the right answer since I got 7435.8eV using a calculator and on the test the approximations would make me even more off.
flyboy621
2010-11-14 19:25:17 |
I think ETS expects you to make the approximation that Yosun did in the solution, i.e. that 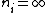 . It makes the math a lot easier, and it gets you the right order of magnitude, which is all you need for this problem. . It makes the math a lot easier, and it gets you the right order of magnitude, which is all you need for this problem.
|
|  | FortranMan
2008-10-19 11:03:03 | Shouldn't it be
)
Where n_{i} is the initial state (either at n_{i}=2 or  ) and n_{f} is the final state (n_{f}=1)? This would explain how the negative cancels out. ) and n_{f} is the final state (n_{f}=1)? This would explain how the negative cancels out. |  | casaubon
2008-10-11 16:41:30 | EDX (Energy Dispersive X-ray Spectroscopy) is a technique to characterize materials based on the wavelength of x-rays emitted from the sample when excited with an electron beam. Beam energy typically needs to be on the order of 10-25 keV to produce a good signal. So, choice D. |  | eshaghoulian
2007-09-15 14:54:25 | Agreed. The solution above is confusing the state of the bombarding electrons with the initial state of the electron making the transition. For minimum energy necessary, the equation is *((Z-1)^2)((1/1^2)-(1/n_{i}^2))) . Minimizing this requires setting . Minimizing this requires setting  (the initial state of the transitioning electron) equal to 2 (note that you can't set it equal to 1 since then you wouldn't have a transition). This minimizes the energy necessary for the transition, and you equate this to the KE of the incoming electron, which isn't making any transitions. So the physical process is: electron comes in from (the initial state of the transitioning electron) equal to 2 (note that you can't set it equal to 1 since then you wouldn't have a transition). This minimizes the energy necessary for the transition, and you equate this to the KE of the incoming electron, which isn't making any transitions. So the physical process is: electron comes in from  , scatters off of an atom by giving up some of its KE, and then the atom makes a transition. , scatters off of an atom by giving up some of its KE, and then the atom makes a transition.
Note the general formula: *((Z-b)^2)((1/n_{f}^2)-(1/n_{i}^2))) . This is a slight modification of Bohr's Law, where . This is a slight modification of Bohr's Law, where 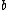 and and 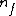 depend on the series you are considering (e.g. depend on the series you are considering (e.g.  DEFINES K series and gives DEFINES K series and gives 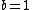 , ,  DEFINES L series and gives DEFINES L series and gives 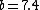 , etc.). The constants , etc.). The constants  should probably be memorized, but I don't predict them asking beyond K or L series (probably won't even ask L series). should probably be memorized, but I don't predict them asking beyond K or L series (probably won't even ask L series).
ali8
2011-06-27 13:46:04 |
Where did you get that eqn from ??
I cannot find it in my Serway Modern Physics Text.
|
blacksheep
2017-09-22 01:12:26 |
Anyone wanting to learn more about this can do a search for \"Moseley\'s Law\" and \"atomic screening constant\" to find lots of information. Here is one interesting document: https://www.ld-didactic.de/literatur/hb/e/p6/p6354_e.pdf\r\n\r\nTransitions to the K shell give rise to the K lines: K-alpha, K-beta, etc. Transitions to the L shell give rise to the L-alpha, L-beta, etc. lines—all very straightforward, notationally. Where it gets interesting is in the calculation of the atomic screening constant (which is usually designated sigma, although eshaghoulian used \"b\"). For an L-alpha line, one would expect sigma to be 9 (representing screening by the remaining n=1 electron and all 8 of the n=2 electrons), but instead it\'s 7.4. You can find a discussion of why here: https://physics.stackexchange.com/questions/208057/how-to-find-the-constants-in-moseleys-law\r\n\r\nThe upshot is that, as with many equations, the one eshaghoulian shared gives an approximate answer.
|
|  | Furious
2007-08-30 18:30:19 | I have to agree with kevglynn, the minimum energy comes at n_i =2 not at n_i goes to infinity. That's actually the MAXIMUM energy.
pam d
2011-09-23 21:19:19 |
No, the electron in the K-shell is being knocked out of the atom by an incoming electron. Therefore it goes from n = 1 (definition of K-shell) to n = infinity (definition of being knocked out). The difference in energy sought in this problem is the minimum energy that an incoming electron must have to do the job.
The actual x-rays produced are the result of L-shell to K-shell transitions (corresponding to n = 2 to n = 1 transitions) of the remaining electrons after the above-described event. The transition could also be an M-shell to K-shell transition. It is even possible that another electron be emitted to carry off the excess energy of this transition rather than an x-ray photon. This is called an Auger electron and it's emission becomes increasingly probable with increasing Z.
|
|  | barefoot0
2006-11-14 11:17:02 | I dont know if this exactly correct but I did the following.
I know 2.5eV gives ~ 500nm (This is just an easy thing to remember and quite usefull).
X rays are about .1 nm and E is inversly proportional to Lambda so
2.5eV*500nm/.1nm ~ 10,000 eV
Someone let me know if and why this method is wrong.
sonnb
2007-05-29 12:49:53 |
The spectrum of X rays ranges from 0.1nm to 10nm so that if you had used 1.0nm instead, you would have gotten the wrong answer.
|
tatitechno
2011-09-19 03:55:48 |
We know that Xray diffraction use about 40Kev in max (reality) so the correct scale is of (D)
|
|  | kevglynn
2006-10-31 11:14:47 | I'm pretty sure that the MINIMUM required energy refers to when the electrons come in from n_i=2. In other words, doesn't n_i refer to the initial state of the electron, not the bombarding electrons? thanks |  | Healeyx76
2006-10-19 18:44:49 | Is there a way to figure out R in Ev if you haven't memorized -13.6eV ? It is not one of the given values at the start of this test.
Oh: I guess you could memorize/know R = (m_e*e^4)/(2*hbar^2) eh?
13.6 13.6 13.6 13.6 ..... have to remember that one.
herrphysik
2006-10-27 21:56:12 |
Definately memorize that number.
|
Setareh
2011-10-24 04:18:23 |
As a physics student, you have to memorize 13.6 just like 2*2=4! I am sure if you deal more with GRE problems you will memorize it, because this number is involved in so many questions.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
