|
GR8677 #17
|
|
|
|
|
Comments |
casseverhart13
2019-09-30 02:48:03 | This is utterly surprising! pressure washing Orlando
danielsw98667
2019-10-21 05:38:21 |
With the given stages of radioactivity, the answer is A. LED bike lights
|
|  | ernest21
2019-08-10 03:09:30 | I would say that muon is a partical from Lepton group so are electron, tauon, neutrino. So the answer must be (A). lol player search |  | joshuaprice153
2019-08-08 07:20:47 | Well, I am so excited that I have found this your post because I have been searching for some information about it almost three hours. You helped me a lot indeed and reading this your article I have found many new and useful information about this subject. air duct |  | jmason86
2009-08-12 21:37:41 | I believe ETS made a typo in the problem statement. The subscript on Y should be Z+1 to be consistent with the rest of the problem.
That is because if Z (the # of protons) decreases by 1, it implies a proton turning into a neutron (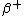 decay). To conserve charge you must emit a positron and to conserve lepton number (from the positron) you must also emit an electron neutrino. decay). To conserve charge you must emit a positron and to conserve lepton number (from the positron) you must also emit an electron neutrino.
In short, p -> n + e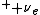
Correct me if I'm wrong :)
segfault
2009-08-22 22:06:46 |
After the *first* stage in the process the subscript should be Z+1, but after alpha emission the subscript becomes Z+1-2=Z-1. This is a two step process.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
