|
GR8677 #84
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
danielsw98667
2019-10-24 04:21:47 | Confused with the value of J. affordableseoservice.org |  | andyferd
2010-11-12 17:35:33 | When is it correct to assume ETS is asking for the spectroscopic notation of the electron rather than the atom? In a problem on a different test they give the spectroscopic notation of an atom and ask for the state of the electron after a transition (I can't remember which other practice test it is) |  | faith
2010-10-23 23:51:18 | there's ambiguity in yosun's solution although it too arrives at the correct answer.
for J
>half filled shell, J=|L+S|
< half filled shell, J=|L-S|
=half filled shell, J=S (since no net orbital momentum)
hence knowing just the value spin which is 1/2, will immediately gives the answer, B. ( and the valence electron is in sub shell s will give notation S)
to clarify S notation can be a lil confusing. S represent spins while S also is use to represent the sub shell s.
|  | wikiwert
2010-09-15 21:55:13 | This excercise is solved using Hund´s Rule; this should be mentioned in the solution (for other atoms, other problems arise, as the one mentioned by student2008). |  | student2008
2008-10-14 03:02:16 | Yosun, you're not quite right writing 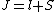 , since , since 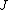 may take any of the values in the range may take any of the values in the range  , separated by 1. , separated by 1.
Otherwise, the information about J would be redundant. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
