casseverhart13
2019-09-20 02:00:25 | It\'s my pleasure to find this amazing problem who provides mostly unseen information about every single problem which is i really like it. tree trimming |  |
ernest21
2019-08-10 03:09:31 | Now i get the point why you use that equation to easily solve the problem. jelly stardew valley |  |
joshuaprice153
2019-08-08 07:24:58 | Spot on with this particular write-up, I truly think this website needs extra consideration. I’ll probably be again to read extra, thanks for that details. event planner Ft Lauderdale |  |
timfinnigan
2018-05-20 03:18:29 | Plug  into the TDSE and then set x=0. You will end up with into the TDSE and then set x=0. You will end up with ^2 / 2M) (should be h-bar). Put that into the TDSE and then cancel like terms. You will end up with V(x)=choice B. (should be h-bar). Put that into the TDSE and then cancel like terms. You will end up with V(x)=choice B.
timfinnigan
2018-05-20 03:19:45 |
This E value will allow you to eliminate choices D&E
|
|  |
GrahamS
2016-10-28 17:37:14 | That doesn\'t give answer E. Answer E has a 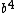 in it, your method (which is the same thing that I did originally) has a in it, your method (which is the same thing that I did originally) has a 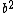 . . |  |
arifmujib
2013-10-13 06:48:24 | The answer should be E . Because 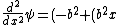^2)\psi) now the kinetic energy part now the kinetic energy part ^2)=E-V(x)=K) now putting x=0 and V(0) = 0 we get now putting x=0 and V(0) = 0 we get =E-V(0)=E) .So the right answer goes to choice E . .So the right answer goes to choice E .
arifmujib
2013-10-13 07:09:42 |
The 2nd EQ will be ^2)=E-V(x)=K) . By the way the choice B was a good candidate for the answer but it requires a minus sign . . By the way the choice B was a good candidate for the answer but it requires a minus sign .
|
arifmujib
2013-10-14 07:56:05 |
Sorry I was wrong . Choice B is the right answer .
|
tjurra
2014-08-25 13:22:22 |
Choice E has 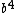 , not , not 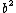 . .
|
QuantumCat
2014-09-02 13:32:47 |
Remember that the term in front of the kinetic is NEGATIVE: 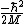
|
GrahamS
2016-10-28 17:37:58 |
That doesn\'t give answer E. Answer E has a 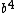 in it, your method (which is the same thing that I did originally) has a in it, your method (which is the same thing that I did originally) has a 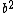 . .
|
gfsampaio
2024-03-12 20:47:37 |
I make for onde form, i get the solution of Schrödinger equation time independent, were the wave function is give for Ψ = A exp(- (2mV(x)/ ℏ²)^1/2 * x), this have to be equal to the wave function given by the question, so (2mV(x)/ ℏ²)^1/2 * x = b²x²/2 resulting in V(x) = ℏ²(b^4)x²/8M. I make problem with this 8M, i don\\\\\\\'t understand for physical interpretation of him, or if i make any basic error in my solution. I see too some answers with the choice E, this is impossible, if E is the right answer, the potential in x=0 is different of 0.
|
|  |
natec
2013-08-15 18:07:19 | why do I get E = (hbar^2)*(b^4)/2M when I plug in V(x)=0 and x=0 (Which is answer E)? Why are the units wrong?
natec
2013-08-15 18:08:12 |
This should be classified as HELP!, haha
|
natec
2013-08-15 18:16:13 |
NEVER MIND. found my mistake; i made a silly mistake with exponents. I actually get E=hbar^2 b^2/2M which is NOT answer E. Sorry for these three useless comments... Thank you for the great website though!
|
|  |
mpdude8
2012-04-15 20:19:31 | You really don't have to know much about QM to get this one. If you know that the terms in the exponent must be dimensionless, the rest is just elimination.
b must have units of 1/length to cancel with x^2. V and E must be in units of Joule, or, using base units, (kg * m^2 / s^2). Knowing that b ~ 1/length quickly tells you the answer must be B without ever invoking the TISE.
Eliminate C immediately because you cannot add or subtract terms with different units.
Also, note that both V and E have the same units -- logically, A and E must both be eliminated, then.
Jovensky
2013-01-20 20:26:18 |
C is fine too by dimensional analysis.
|
|  |
deafmutemouse
2011-11-08 18:36:51 | I agree with Kabuto Yakushi more or less. Couldn't you just plug  into the TDSE? Then the solution falls out. into the TDSE? Then the solution falls out.
oliTUTilo
2012-11-01 16:13:05 |
You could use the time-dependent SE, but this only adds to the already long problem. Kabuto Yakushi has stated that 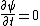 , but this is misleading since the time derivative of , but this is misleading since the time derivative of 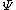 (\psi muliplied by the time component of the wavefunction) isn't zero and we must use it if we want to apply the time-dependent SE. In fact, since (\psi muliplied by the time component of the wavefunction) isn't zero and we must use it if we want to apply the time-dependent SE. In fact, since 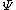 is an eigenfunction, it must be of the form is an eigenfunction, it must be of the form  , which would make (Time dependent SE) , which would make (Time dependent SE) 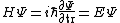 . The hamiltonian operator for this system, H, has no time dependence, and so this reduces to the time-independent SE, . The hamiltonian operator for this system, H, has no time dependence, and so this reduces to the time-independent SE,  , and we're back at square one. , and we're back at square one.
Using 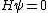 , as Kabuto suggests, would give me an incorrect result...maybe the fixed-typo some people are talking about has something to do with it. , as Kabuto suggests, would give me an incorrect result...maybe the fixed-typo some people are talking about has something to do with it.
|
|  |
ali8
2011-06-23 05:56:14 | In the solution, why is the term -b^2 omitted?
drizzo01
2012-10-23 11:53:50 |
it was a typo. There when the B.C. was applied, all x=0, so really all that should have remained was the -b^2 term. The rest follows
|
|  |
walczyk
2011-04-06 17:07:23 | I understand the source of the confusion I think. It isn't necessarily a typo but a confusion in the accepted solution. E cannot depend on x, so the quadratic term generated by the kinetic energy term in the SE must be eliminated by the potential energy term. So folks, the constant term  is IN FACT the eigenvalue of the energy of the system. The answer makes it seem that plugging in the given conditions for the potential makes is IN FACT the eigenvalue of the energy of the system. The answer makes it seem that plugging in the given conditions for the potential makes 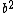 disappear, but no, that's not it. Check again. The conditions given in the problem lets us not worry about any constant potential term that would modify eigenvalues at the end. Its not really that helpful. Just the knowledge that the energy must not depend on disappear, but no, that's not it. Check again. The conditions given in the problem lets us not worry about any constant potential term that would modify eigenvalues at the end. Its not really that helpful. Just the knowledge that the energy must not depend on  is enough for you to choose the right answer, after you plug and chug of course. is enough for you to choose the right answer, after you plug and chug of course. |  |
Almno10
2010-11-11 13:53:44 | One way to look at this is that
i) E cannot depend on x
ii) V(0) = 0
B is the only option which satisfies i and ii.
pam d
2011-09-23 20:21:08 |
Actually this line of reasoning only eliminates (A) and (D). It certainly helps to make these eliminations, but there are more steps.
|
|  |
alemsalem
2010-09-20 07:42:47 | from the Schrodinger equation it is obvious that the units of energy are same as the units of h^2/(2m dx^2) all the answers should have a unit of energy b has units of inverse length ,, this leaves B and C.
a Gaussian wave-packet has a shape like this (at t=0) but it's not an eigenstate of the equation, and it must be a harmonic potential anyway (ground state).
also if you derive the wave function twice you can easily tell that at most you will get x to the power of 2 and because energy should be a constant for all x the potential cannot turn out to have x^4. |  |
Kabuto Yakushi
2010-09-02 09:49:11 | I just plugged the wave function into the schrodingers equation.
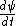 is obviously zero so V(x) is obviously zero so V(x)
equals the second time derivative of psi time the
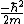 . Solving one gets B). . Solving one gets B).
Thanks for the great site Yosun.
arifmujib
2013-10-13 06:57:50 |
Usually the simple form of SE(schrodingers equation) we work with is the space part of the real SE . The actual wave equation  = \psi (x) \phi (t)) we work with the time independent part we work with the time independent part ) . The SE we have here is a time independent SE . So your calculation is wrong . . The SE we have here is a time independent SE . So your calculation is wrong .
|
|  |
Plantis
2010-04-06 05:42:52 | I don't agree with solution. When we are plugging the potential conditions V(x)=0 and x = 0. It's mean that we will recieve (A) correct answer.! I don't clearly understand the solution.
apr2010
2010-04-09 06:49:32 |
After you get  = E) as Yosun describes you have to calculate as Yosun describes you have to calculate
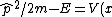) which will give answer B). which will give answer B).
|
faith
2010-10-25 19:48:53 |
there is a typo in yosun;s solution.rnrnplugging in V(0) would require E to be just h^2*b^2/2m = E (which was commented by marshiesbudda). solving that you'll arrive at the answer of B
|
|  |
physics_gre
2009-12-24 02:33:42 | the given vave function is in the usual form of a one dimensional linear harmonic oscillator.we know the expression for the potential of a lho is
v(x)=(1/2)kx.x.so the correct answer is b.
|  |
solarclathrate
2009-08-24 00:28:17 | I don't quite understand the final implication in the solution. Is he trying to say that because the energy is independent of  , the only way for , the only way for =0) is for answer B to be true? is for answer B to be true? |  |
evanb
2008-06-18 17:43:24 | (A) can be eliminated based on given knowledge that V(x=0) = 0, except in the pathological b = 0 case.
(C) can be eliminated based on knowledge that the potential is harmonic.
(D) can be eliminated because an eigenfunction of the SE has a constant E, not one that varies based on position.
(E) can be eliminated based on units: just assume [E] = [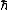 ] [ ] [ ]. Then, check if [ ]. Then, check if [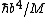 ] has units of 1/s. ] has units of 1/s.
Therefore it must be (B).
ssp
2008-09-05 03:07:22 |
Just to add to the "Elimination" time
For (C) just think about applying the 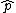 to see that you can never get to see that you can never get 
For (D) you just have to look at the units after the V(x) = 0 condition is applied. You get 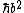 doesn't look like an energy to me... doesn't look like an energy to me... 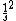
For (E)... Why do we need to know about the potential for this one? ETS and useless information... kick it
|
pam d
2011-09-23 20:23:47 |
ssp, you cannot eliminate (E) like that. They are asking for what statement is correct. Choice (E) is certainly incorrect but not for the reason you are using. evanb's reasoning is much more sound.
|
|  |
barefoot0
2006-11-14 10:32:18 | Would you not plug 0 in for x and thus V(0)-> 0 and then whatever remains on the left side must be E. Then by subtracting E when x =/ 0 gives us the V term?
In other words h^2*b^2/2m = E + V(0) = E,
E + V(x) - E = h^2*(b^2 x)^2/2m
or am I wrong? |  |
transoid
2006-05-05 10:14:05 | No, there is no typo. The solution did say "This implies that the term on the left that disappeared from that substitution is the V(x) term". Thus you have to put E back in to find out V(x). |  |
marshiesbudda
2006-02-20 14:00:04 | There is a typo in the solution. plugging in v(0)=0 gives you h^2*b^2/2m = E |  |
tarlen
2005-11-30 21:17:28 | While this solution is very illuminating, a very quick way of solving this one is to realize that this wavefunction is a gaussian wave packet. There are only 2 potentials that give a Gaussian wave packet: one is the free particle and another is the ground state wavefunction of the harmonic oscillator potential. Since the free particle potential isn't there, we know the answer must be b), the harmonic oscillator potential.
kicksp
2007-10-29 10:29:11 |
Watch out! The given wave function is NOT a Gaussian wavepacket. And a constant potential (A) can yield "free-particle solutions": plane waves.
|
sirius
2008-11-05 20:17:00 |
tarlen is mostly correct. It is not a wave packet however, since it is not in motion as in the free particle. It is simply a gaussian, which is characteristic of a harmonic potential. So (B).
|
alemsalem
2010-09-20 07:24:28 |
the Gaussian wave packet isn't an eigenstate of the Schrodinger equation
|
|  |
