|
|
|
| All Solutions of Type: Optics | | 1 | Click here to jump to the problem! | GR8677 #58
|
Optics }Holograms }Holograms
A hologram is produced from interference of light. Interference of two-beams (one going directly to the film, the other bouncing off the object) produced by a beam-splitter allows the film to record both intensity and relative phase of the light at each point. Intensity (to wit: 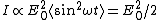 ) does not depend on angular frequency, but only on phase and amplitude. Thus, choice (B) is right. ) does not depend on angular frequency, but only on phase and amplitude. Thus, choice (B) is right.
|
| 4 | Click here to jump to the problem! | GR8677 #91
|
Optics }Bragg Reflection }Bragg Reflection
Bragg diffraction is basically the wavelength change of a wave impinging two adjacent layers of the crystal. More specifically, it relates the wavelength difference of the incident wave on the top layer to that of the reflected wave on the lower layer. The distance between layers (``lattice planes", in Solid-State-Speak) is  , and the angle of incidence is , and the angle of incidence is  . The change in wavelength is thus a simple geometry problem, the result being the celebrated Bragg Reflection Relation, . The change in wavelength is thus a simple geometry problem, the result being the celebrated Bragg Reflection Relation,

where  corresponds to the order of the reflection. corresponds to the order of the reflection.
The problem supplies the following numbers
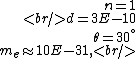
and if one recalls the de Broglie relation, 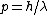 , one has, in general, , one has, in general, 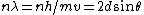 . Plugging in some numbers, one finds that . Plugging in some numbers, one finds that 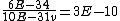 , since , since 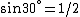 , and where the approximation scheme to battle the no-calculators-allow requirement is shown. Thus, one has , and where the approximation scheme to battle the no-calculators-allow requirement is shown. Thus, one has 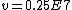 , which is very close to choice (D). , which is very close to choice (D).
The problem .
|
| 10 | Click here to jump to the problem! | GR8677 #58
|
Optics }Lensmaker Equations }Lensmaker Equations
Although this problem mentions lasers, no knowledge of quantum mechanics or even lasers is required. Instead, the problem can be solved as a simple geometric optics problem using the lensmaker's equation, 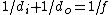 , relating the distances of the object, image, and the focus. , relating the distances of the object, image, and the focus.
Since there are two convex lenses, one can treat the set-up as a telescope. The lens closest to the laser is the objective (with focus 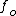 ) and the one closest to the bigger-radius well-collimated beam is the eyepiece ) and the one closest to the bigger-radius well-collimated beam is the eyepiece  . .
The laser-light comes in from 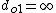 , and thus one has , and thus one has 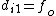 , i.e., the image forms at the focal point. , i.e., the image forms at the focal point.
Using the telescope equation, one has 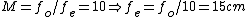 , since one wants a final magnification of 10 (to wit: input beam is 1mm, output beam is 10mm). This narrows down the choices to just (D) and (E). , since one wants a final magnification of 10 (to wit: input beam is 1mm, output beam is 10mm). This narrows down the choices to just (D) and (E).
Since the distance between lenses for a telescope (with incoming light coming from infinity) is given by 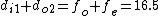 , which relates the distance of the image from the first lens to the distance of the object from the second lens, one arrives at choice (E). (Correction due to user tachyon.) , which relates the distance of the image from the first lens to the distance of the object from the second lens, one arrives at choice (E). (Correction due to user tachyon.)
|
| 14 | Click here to jump to the problem! | GR8677 #13
|
Optics }Aperture Formula }Aperture Formula
The circular aperture formula (a.k.a. Rayleigh Criterion) is given by 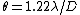 . Plug in the given quantities to get that. . Plug in the given quantities to get that.
(It's a nice formula to memorize, as it's used as common sense in a variety of engineering fields, as well as in remote-sensing, such as satellite-communications.)
|
| 18 | Click here to jump to the problem! | GR8677 #97
|
Optics }Refraction }Refraction
From Snell's Law, one obtains  \sin\theta^{'}) , since the index of refraction of air is about 1. , since the index of refraction of air is about 1.
Now, differentiate both sides with respect to  . .
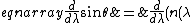 \sin\theta^{'})\\
0&=& \frac{dn(\lambda)}{d\lambda} \sin\theta^{'}+(n(\lambda) \cos\theta^{'}) \frac{d\theta^{'}}{d\lambda}\\
\delta \theta^{'} &=& |\tan\theta^{'}/n \frac{dn(\lambda)}{d\lambda} \delta \lambda|, <br />
\end{eqnarray})
which gives choice (E) to be the angular spread.
This solution is due to ShyamSunder Regunathan.
|
| 19 | Click here to jump to the problem! | GR8677 #100
|
Optics }Interferometer }Interferometer
This is a nice problem.
An interferometer, like its name suggests, has to do with interference. Namely, it splits light-beams through the beam-splitters (BS) half and half, then recombines them at the end---the end result shows interference which varies depending on whether the moveable mirror is placed a quarter of a wavelength away (so that the path difference, which is twice that, is half a wavelength).
A fringeshift occurs whenever  . Thus . Thus 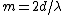 , where m is the number of fringes and , where m is the number of fringes and  is the wavelength. is the wavelength.
Using the information for the red beam, one can find 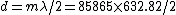 . Applying the same equation for the green beam, one finds that . Applying the same equation for the green beam, one finds that 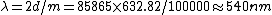 , as in choice (B). , as in choice (B).
|
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
