danielsw98667
2019-10-21 06:43:43 | 3N oscillators - Phonons for Debye - A different version. Armor Services Roofing |  |
casseverhart13
2019-10-07 03:44:16 | First-class problem it is really. remodeling |  |
fredluis
2019-09-17 01:54:27 | does it depend on interger or fractional quantum hall effects? tree removal |  |
ernest21
2019-08-23 02:02:31 | This question is classical in nature. cartoon wars 3 |  |
849444209
2013-10-16 06:43:31 | 嗯,爱因斯坦太懒了
Cambs01
2016-09-14 15:38:22 |
I wonder why you have to make this comment which is not related to the question. I assume everyone is encouraged to use English on this website. (btw I am Chinese too.
|
godkun
2017-04-03 19:31:06 |
你是傻逼吗?儿子?
|
zengwl17206
2017-09-08 22:42:01 |
You\'d better delete the comment.
|
tommy22222
2019-10-13 04:23:36 |
I dont see any problem with 849444209\'s comments. This website is intended for audiences from all over the world. If he chooses to make a remark in a language which he feels comfortable with, there is no problem with it. Not disturbing at all from my perspective.
|
|  |
Pumpkin
2010-04-03 18:46:09 | What I'm concerning is 'independent' harmonic
oscillators - In Debye theory of solid, H.O.s are
not independent and that actually makes difference
as you guys arleady referred.
Of course it specified 'vibrational energy', so still
the nearest choice may be (B), but I don't think
it is nice and smooth problem.
kronotsky
2018-10-23 04:23:24 |
In classical regimes, equipartition of energy.
|
|  |
Altair
2005-11-11 09:07:25 | "Einstein was too lazy" is an amazing comment! Although it is almost offensive :-) the result is sure: I'll never forget Einstein decided that the oscillators have the same frequency!
yosun
2005-11-11 14:21:06 |
altair: here's another bit of irreverent trivia---Einstein's 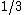 -arsed theory did not produce the right specific heat for low temperatures, and thus deBye's theory, which gave the right resulst for both low and high temperatures, prevailed (recall the -arsed theory did not produce the right specific heat for low temperatures, and thus deBye's theory, which gave the right resulst for both low and high temperatures, prevailed (recall the 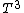 law for low temperatures). law for low temperatures).
|
|  |
