|
GR8677 #100
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-07-16 13:39:56 | Interesting and very rattling problem. Bookmarked. www.partnersairductcleaning.com/beverlyheights33301 |  | Simplicio
2009-03-31 18:51:18 | I would agree with hungrychemist and consider the order of magnitude.
The reasonably values I used are
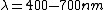 , , 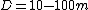
(A)  ≈ ≈ 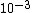
(B) 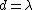 : Good luck making a camera pinhole the size of the wavelength ... : Good luck making a camera pinhole the size of the wavelength ...
(C) 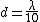 : This is even worse! : This is even worse!
(D) 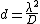 : LOL! : LOL!
(E) 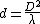 : Can this even be called a "pin"-hole? : Can this even be called a "pin"-hole?
So by elimination, (A) gives a small yet reasonable number! |  |
|
|
Comments |
Cheese
2019-09-24 13:22:34 | So I was out of time when I saw this question in my attempt, I though that the quantity \"Sharpness\" could be just a numerical measure (and hence dimensionless) much like how \"magnification\" is treated in optics, so I just locked (A) only for that reason. |  | casseverhart13
2019-07-16 13:39:56 | Interesting and very rattling problem. Bookmarked. www.partnersairductcleaning.com/beverlyheights33301 |  | calvin_physics
2014-03-27 22:39:05 | Just like others have suggested,
answers from B to E are simply silly if we apply some logic to it.
Visible lights has wavelength 400~700nm
Distance for an image is usually few meters.
Only (A) gives few millimeter as answer, which fits the description of pinhole. |  | syreen
2013-09-23 18:45:05 | I used rayleigh criterion and small angle approx:
Rayleigh-
sin(theta)=~theta=lambda/d
small angle-
theta~=arclength/distance~="blur"/D
Set the two theta equations equal, solve for blur, then
derivative of blur with respect to d, set to 0 to minimize blur. Solve for d. gives A. |  | mpdude8
2012-04-19 17:18:46 | Yeah, bag all the optics and look at it logically. If you know the wavelength of light is on the order of nanometers, a pinhole, while small, is probably on the order of millimeters, and the screen, probably on the order of centimeters, you can use orders of magnitude to figure out which answers are possible and which are nonsense. |  | rizkibizniz
2011-10-07 02:10:00 | tho im quite sure Yosun's answer is more accurate, but all this PGRE stuff is about approximation isn it? can someone point out why its a big mistake to approximate using Rayleigh's criterion? |  | rizkibizniz
2011-10-07 02:01:41 | couldn' we approximate all this just using Rayleigh's criterion? for sharp images, (to be able to distinguish two separate objects with small angle  ) : ) :
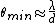 , ,
 , ,
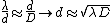
Setareh
2011-10-29 01:07:31 |
Nice!
|
rizkibizniz
2011-11-06 21:28:13 |
Hmm. I come to realize that I have mistakenly defined  which doesn seem to be the correct reasoning to get the angle subtended by the objects through the pinhole on the screen which is what which doesn seem to be the correct reasoning to get the angle subtended by the objects through the pinhole on the screen which is what 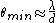 is.rnrnWhat I had (mistakenly) defined was the angle subtended by lines from the edges of the pinhole to a point on the center of the screen. rnrnI think it might be a coincidence that the answers came out to be similar if not the same. Or can they both be in fact the same to some certain approximations? Anyone have any thoughts on this? is.rnrnWhat I had (mistakenly) defined was the angle subtended by lines from the edges of the pinhole to a point on the center of the screen. rnrnI think it might be a coincidence that the answers came out to be similar if not the same. Or can they both be in fact the same to some certain approximations? Anyone have any thoughts on this?
|
livieratos
2011-11-08 07:30:56 |
i think that this is the case:
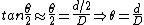
somebody correct me if i'm wrong please...
|
ewcikewqikd
2014-07-19 12:41:00 |
The problem with ur solution is that the "d" in the single slit equation is the width of the slit (pinhole), not the width of the screen. The width of the pinhole is never given in the problem.
|
|  | Simplicio
2009-03-31 18:51:18 | I would agree with hungrychemist and consider the order of magnitude.
The reasonably values I used are
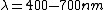 , , 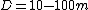
(A)  ≈ ≈ 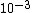
(B) 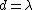 : Good luck making a camera pinhole the size of the wavelength ... : Good luck making a camera pinhole the size of the wavelength ...
(C) 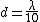 : This is even worse! : This is even worse!
(D) 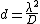 : LOL! : LOL!
(E) 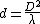 : Can this even be called a "pin"-hole? : Can this even be called a "pin"-hole?
So by elimination, (A) gives a small yet reasonable number!
flyboy621
2010-11-15 20:48:43 |
Nice!
|
|  | thebigshow500
2008-10-14 09:44:48 | Not sure if this make sense: Can we simply apply single slit diffraction's equation?
1. 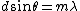
Let m=1 to let the sharp image reach its 1st order minima, and then we have
2. 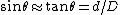
For the Fraunhoffer diffraction,  so that we can assume a small angle. so that we can assume a small angle.
Plug 2. back to 1., and we eventually get
 = \lambda)

medellin
2008-11-04 13:01:09 |
I think you got the answer just by chance, but there is not really physics there. I think your procedure got the answer just by the orders of magnitude involve but no more.
|
medellin
2008-11-04 13:02:53 |
You need FRESNEL DIFFRACTION as mentioned below.
|
tinytoon
2008-11-06 00:04:52 |
Actually, your solution makes perfect sense, physically also.
|
h.fei10
2012-11-07 22:14:23 |
I think, in your second equation, you should use the radius of the blur, not just the diameter of the pinhole. It doesn't make sense.
|
ewcikewqikd
2014-07-19 12:38:12 |
The problem with ur solution is that the "d" in the single slit equation is the width of the slit (pinhole), not the width of the screen. The width of the pinhole is never given in the problem.
|
|  | Richard
2007-11-01 18:55:36 | I did this one by relying on my intuition, namely, that if we increase the distance the screen is from the hole, the optimum diameter of the hole should increase, and also that if you let the wavelength become very large
the diameter of the hole should increase to get a resolved image. The only solution that fits this is (A).
For those wondering what is meant by "blur," it may be useful to look at the site Yosun quoted/pirated. "Blur" is basically a quantification of the interference on the image, how much "blur" there is. There is interference due to incident light entering the hole and interference due to diffraction around the hole's edges. These combine as Yosun quotes and the sum's minimum is obtained by a differentiation.
|  | hungrychemist
2007-09-17 08:00:32 | Use order of magnitude approach. Say, if we set  = 1 unit of length. D is about 10^8 of that same unit. (Size of camera should be in order of m where the size of the visible light wave length is order of nm).rnrnNow, you want d (pin hole size) at the order of 10^-2 or so. (About size of mm). rnrnChoise E is way too big(bigger than the camera)rnChoice D is way too smal(smaller than the wavelength of light)rnChoice C is still too small(still smaller than the wavelength of light)rnChoice B is same as wavelength of light(still quiet small, and we know from double slit experiment, this magnitude of hole will create dispersion of wave, which blurs things). rnChoice A is only reasonable magnitude. = 1 unit of length. D is about 10^8 of that same unit. (Size of camera should be in order of m where the size of the visible light wave length is order of nm).rnrnNow, you want d (pin hole size) at the order of 10^-2 or so. (About size of mm). rnrnChoise E is way too big(bigger than the camera)rnChoice D is way too smal(smaller than the wavelength of light)rnChoice C is still too small(still smaller than the wavelength of light)rnChoice B is same as wavelength of light(still quiet small, and we know from double slit experiment, this magnitude of hole will create dispersion of wave, which blurs things). rnChoice A is only reasonable magnitude. |  | yosun
2005-10-31 01:14:19 | Fresnel Diffraction would complicate things. Franhouffer should be a good approximation, especially when one has only about a minute to answer the question.
alpha
2005-10-31 12:47:49 |
Shouldn't Fresnel Diffraction be used instead, as 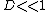 ? ?
|
ee7klt
2005-11-11 04:44:44 |
Hi Alpha,
I think the question says 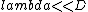 , thus justifying the Fraunhofer regime. , thus justifying the Fraunhofer regime.
I have one question, why is reasoning behind defining the blur equation as written?
|
ee7klt
2005-11-11 04:45:27 |
oops..I meant "what is the reasoning.."
|
student2008
2008-10-14 07:38:54 |
the condition  is needed to neglect the second term under the square root in the Fresnel zones formula: is needed to neglect the second term under the square root in the Fresnel zones formula: 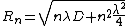
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
