|
GR8677 #69
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-08-29 02:53:50 | Merely a smiling visitant here to share this problem! tree trimming |  | ben
2006-07-19 15:54:53 | i think an easier way to do it that gives the exact answer without having to memorize a table is to simply solve for v explicitly in the equation 3/sqrt(1-v^2/c^2)=5. just square both sides and you'll find that v^2/c^2=16/25 at which point the answer is obvious. |  |
|
|
Comments |
casseverhart13
2019-08-29 02:53:50 | Merely a smiling visitant here to share this problem! tree trimming |  | RusFortunat
2015-10-21 16:04:12 | Just a little typo. At last string you have $\\beta >0.75c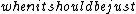 \\beta >0.75$ \\beta >0.75$ |  | wittensdog
2009-10-07 16:20:35 | I've found a way that works for me for remembering how to get the velocity when the lorentz factor is known. If b is the velocity in units of c, aka, v/c, and g is the lorentz factor, then we have,
g = [ 1 - b^+2] ^ - (1/2)
b = [ 1 - g^-2 ] ^ +(1/2)
after working through the math. The way that I remember it is that if you take one of them, swap b and g, and then swap the exponent signs, you get the other one. So they have some kind of nice antisymmetry, or whatever you want to call it.
Hope this helps someone... |  | barefoot0
2006-11-27 12:23:00 | But 16/25 is .64 not .8 so you would get answer B instead. But ETS said answer C is correct.
barefoot0
2006-11-27 12:25:13 |
never mind I forgot to take the square root.
|
|  | nitin
2006-11-21 04:19:22 | trombone,
I think you need to check yourself out. You're acting like a kid, and your aim is clearly to insult me, which is a shame since I did not address you in anyway. Your attitude is that of a moron, and Lubos Motl has given a good definition of it. |  | nitin
2006-11-16 11:25:38 | Another nonsensical solution...
Ben is right, and I simply don't understand why you decide to change from the fractional form "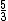 " to the decimal form " " to the decimal form "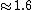 ", which drives you into a long mess! ", which drives you into a long mess!
trombone
2006-11-18 19:16:45 |
The only nonsensical thing here is you bitching about the method that was used. Post a better solution if you have one, otherwise stop whining.
|
|  | tera
2006-08-13 07:38:59 | The comment of ben is quite correct iti isd very simply because the square roots become precise
|  | ben
2006-07-19 15:54:53 | i think an easier way to do it that gives the exact answer without having to memorize a table is to simply solve for v explicitly in the equation 3/sqrt(1-v^2/c^2)=5. just square both sides and you'll find that v^2/c^2=16/25 at which point the answer is obvious.
Goddar
2009-10-04 23:13:11 |
Same here, i find it very useful on this type of question to express gamma as a fraction:
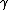 = = 
Then in units of c:
v = 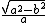
Saves precious time.
|
shak
2010-07-31 21:27:32 |
that is the easiest way! i dont understand why Yosun approached this problem in a very complicated way
|
neon37
2010-11-03 12:07:17 |
Goddar, thats a neat trick. Saves few precious seconds! It's simplicity makes me say... why didnt I think of that!
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
