|
GR8677 #96
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-08-12 07:04:10 | I’d been just browsing every now and then and also got to learn to read this problem. power washing |  |
|
|
Comments |
casseverhart13
2019-08-12 07:04:10 | I’d been just browsing every now and then and also got to learn to read this problem. power washing |  | GRE0717
2015-10-20 21:28:08 | I couldn\'t figure why the odd terms would give zero coef cause n=1 ,3, 5,... for square well are even functions. The question had n=0 as the ground state instead, so everything shifted by -1. |  | neo55378008
2012-09-06 13:11:22 | All the odd n's should have a node at the middle of the well. If there is a voltage at zero, the wavefunctions will be altered.
Did I over simplify this too much? |  | Donofnothing
2010-10-05 07:53:43 | one thing i've always had trouble with is guessing if ETS is starting with n=0 or n=1 for ground states in these kinda problems. in this one, look at the index on the summation. it's starting at 0, so that means 0 is your ground state!rn
wavicle
2011-11-08 14:37:14 |
Yes it's so silly. Technically you don't have to guess, just read carefully. But seriously. The energy for infinite square well goes as n^2 with the ground state being nonzero. Hence if n=0 corresponds to ground state, to do an energy calculation, in code for example, you would have to offset by 1. Then again, if you live in an ivory tower and only do math on paper, what does it matter to you?
|
|  | mangree
2008-10-18 08:19:55 | To sum it up,because there is a lot of misunderstanding about this:
V and V' are both even,so the perturbed potential V+V' is even.
Therefore the perturbed problem has even AND odd eigenfunctions.
The (new) groundstate however is even,thus it is a mixture of even states only  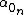 =0 for n=1,3,... =0 for n=1,3,...
Saint_Oliver
2013-09-14 14:05:41 |
This is an important point. Eigenfunctions of both the unperturbed and the perturbed potential will have both symmetric and antisymmetric members. The key in this problem is that it is asking about the ground state, which will be composed of only the symmetric eigenfunctions.
|
|  | magneton
2008-09-28 21:06:14 | The unperturbed ground state wave function is even.
The perturbed wave function must remain even in ALL orders of the perturbation theory. Explanation:
the matrix elements of the perturbation potential V' (it is an even function of x, depending on |x| only) are only between the states of the SAME parity: even-even or odd-odd. Since the unperturbed ground state wave function is even, only the states with even n =0, 2, 4, ... are admixed to it. Therefore, all a_0n with odd n must be zero, as in C. |  | kolahalb
2007-11-21 17:43:42 | Friends,the symmetry in the potential must reflect in the form of the wave function.
Here,the potential is even.=>The wave-functions are even=>odd terms are zero.
Poop Loops
2008-09-23 20:49:00 |
Okay, but the non-perturbed potential is also even, yet you get wave functions that are odd. I am not understanding why even potential = even wave function.
|
mangree
2008-10-18 08:11:15 |
Even potential  the eigenfunctions of the problem are even AND odd. the eigenfunctions of the problem are even AND odd.
|
p40515
2010-10-01 14:59:07 |
symmetric perturbation potential  all even and odd eigenfunctions will keep their geometric characteristic after perturbation all even and odd eigenfunctions will keep their geometric characteristic after perturbation  ground state,that was even, will be even after per....rnbut remember to ignore unperturbed ground state from series in the answer;this is at most true(because of the first-order perturbation formula showing perturbed eigenstate) ground state,that was even, will be even after per....rnbut remember to ignore unperturbed ground state from series in the answer;this is at most true(because of the first-order perturbation formula showing perturbed eigenstate)
|
lelandr
2011-04-26 11:07:17 |
I would like to try and clarify some things:
1) An even potential does NOT mean that all of the eigenfunctions will be even.
2) An even potential DOES mean that the square of the wave function will be even.
3) An even potential DOES mean that the GROUND STATE wave function will be even.
so in fact - "Here,the potential is even.=>The wave-functions are even=>odd terms are zero." is not correct.
I believe this could more accurately read:
Here the potential and the perturbing potential are both even -> the perturbed GROUND STATE wave function will also be even -> If we write this as a linear combination of our non-perturbed basis of wave-functions, we can write this using only the even-wave functions (which here are the EVEN terms - thus the ODD coefficients are 0)
|
|  | Richard
2007-11-01 13:16:41 | I like Yosun's solution.
Jeremy
2007-11-02 18:04:10 |
I think the first paragraph is great. My trouble is with the second paragraph. In my opinion, it's almost assuming the reader knows how to solve the problem. If I've looked up the right answer, I already know that the sum does not contain odd terms, and that I must work my way towards this or another equivalent statement. Now, let's say I represent someone who took the test, got the problem wrong, and then came to this page for an explanation (which is, in fact, true). Could I not solve the problem because I failed to realize that 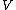 or or 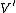 are even? Maybe, but it's more likely that I couldn't figure out why this eliminated the odd terms in the sum. However, this is not explained. And there's no mention of the strange convention being used in the indices. I guess the short way of putting it is "This solution didn't help me." I've learned a lot of physics using this site, but the explanations here fell short of the typical quality and clarity. are even? Maybe, but it's more likely that I couldn't figure out why this eliminated the odd terms in the sum. However, this is not explained. And there's no mention of the strange convention being used in the indices. I guess the short way of putting it is "This solution didn't help me." I've learned a lot of physics using this site, but the explanations here fell short of the typical quality and clarity.
|
|  | tin2019
2007-10-29 09:11:05 | Well let's TeX out the derivation in case somebody needs it. We are supposing that our Hamiltonian is a sum of an unperturbed hamiltonian which is 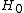 and a small pertubation and a small pertubation 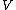 . Then our stationary Schrodinger equation becomes . Then our stationary Schrodinger equation becomes
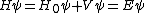 . .
As the solutions of the unperturbed system make a complete set of functions our function of the perturbed system must be a superposition of the functions }_n) , i.e. solutions of the equation , i.e. solutions of the equation 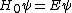 . In other words . In other words
}_n) . .
Replacing this into our initial Schrodinger equation we get
}_n+ V\sum_n a_n\psi^{(0)}_n=E\sum_n a_n\psi^{(0)}_n)
or
}_n+ \sum_n a_nV\psi^{(0)}_n=E\sum_n a_n\psi^{(0)}_n) , ,
where 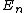 are energy levels of unperturbed system. We now multiply both sides by are energy levels of unperturbed system. We now multiply both sides by }_m^*) and integrate to get and integrate to get
*}V\psi^{(0)}_ndV=Ea_m)
or
+ \sum_{n\ne m} a_nV_{mn}=0) . .
where *}V\psi_n^{(0)}dV) It would be beneficial to memorize this result for the future as from it is easier to proceed with almost any problem conserning perturbation. Note that had the problem been the one with degenerate eigenstates the result would be somewhat different, as our development would have to include eigenfunctions with the same eigenvalue of energy. Now we expand It would be beneficial to memorize this result for the future as from it is easier to proceed with almost any problem conserning perturbation. Note that had the problem been the one with degenerate eigenstates the result would be somewhat different, as our development would have to include eigenfunctions with the same eigenvalue of energy. Now we expand 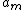 and and  into series, i.e. into series, i.e. }+a_m^{(1)}+...) and and }+E^{(1)}+...) . Note that our perturbation can be expanded into series where the zeroth term would be zero, as the zeroth term corresponds to no perturbation. For the first order perturbation we have: . Note that our perturbation can be expanded into series where the zeroth term would be zero, as the zeroth term corresponds to no perturbation. For the first order perturbation we have:
}(E_m-E^{(0)}+a_m^{(1)}(E_m-E^{(0)})+a_mV_{mm})+\sum_{n\ne m +\sum_{n\ne m}a_n^{(0)} V_{mn}} =0) . .
The level of interest is the ground level state. For a ground state we then have that the zeroth order coefficients are zero for every 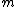 except except 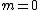 , i.e. that our unperturbed ground state wavefunction has only one term in the expansion, namely itself. Now it follows that for , i.e. that our unperturbed ground state wavefunction has only one term in the expansion, namely itself. Now it follows that for 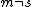 we have we have
}(E_m-E^{(0)})+ V_{m0}}=0)
or that
}=\frac{V_{m0}}{(E_m-E^{(0)})}=0) . .
As the unperturbed ground state is an even function and the perturbation is an even function we have that 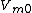 are zero for are zero for 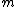 such that such that }) is odd. This is true for is odd. This is true for 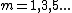 , therefore the coefficients vanish for odd , therefore the coefficients vanish for odd 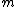 . .
kb
2007-10-29 14:44:57 |
yes i agree u just showed that the coefficients vanish when m = odd for the first order correction.
but the old unperturbed wavefunction does not change so the total wavefunction (psi0 + correction) must still contain both even and odd terms.
but my problem is i think the question its very ambiguous when it askes for psi' , is that the total wavefunction or only the correction part?
|
|  | kb
2007-10-24 19:16:27 | I am confused, if this question is asking for the TOTAL (psi0 + psi1) perturbed wavefunction, not simply the first order CORRECTION... then all even and odd wfs should remain because the perturbation is so small...
only the odd terms in the CORRECTION should go away, not the actual wavefunction
Jeremy
2007-11-02 17:16:21 |
You bring up an important point that I hadn't thought of. I have already argued for why the first order correction for the ground state, psi1 as you put it, is even. Your psi0 we already know to be even*. Therefore, psi0 + psi1 is even, as expressed in answer choice (B).
* The ground state wave function for a well spanning 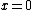 to to 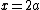 (I would use (I would use  , but , but 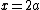 keeps the same well width as the test problem) is: keeps the same well width as the test problem) is: ) . You can get the ground state for this potential (the unperturbed one) using . You can get the ground state for this potential (the unperturbed one) using 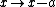 , so that , so that =\sqrt{\frac{1}{a}} \cos\left( \frac{\pi}{2 a} x \right)) , which is indeed an even function. , which is indeed an even function.
|
|  | Jeremy
2007-10-10 12:23:25 | This problem is EVIL! I picked (C) on this problem. I spent quite a while trying to figure out why (B) is right; and it was only when I got around to writing some equations down that I realized I had fallen for a subtle trap: THIS PROBLEM USES N=0, NOT N=1, FOR THE GROUND STATE!!! So of course I get the wrong answer because I'm thinking even  produces an odd wave function, but just the opposite is true - you get an even wave function. produces an odd wave function, but just the opposite is true - you get an even wave function.
Also, the explanations on this page are weak at best, unless perturbation theory is a fresh topic in your mind. Not that I'm about to throw down a derivation, but here is the pertinent formula:
} \psi^{0}_{m}) , ,
where 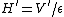 (See Griffiths 6.1, problem 6.1 (b) might give you deja vu). This is the first-order correction to the wave function - not what the question is asking for, but close enough I think because the perturbation is "very small." The bracket represents the integral of the product of the three functions shown. (See Griffiths 6.1, problem 6.1 (b) might give you deja vu). This is the first-order correction to the wave function - not what the question is asking for, but close enough I think because the perturbation is "very small." The bracket represents the integral of the product of the three functions shown.  is even (about the center of the well). We're after the new ground state ( is even (about the center of the well). We're after the new ground state (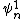 ), so ), so 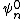 is the unperturbed ground state - another even function. Thus, the parity of is the unperturbed ground state - another even function. Thus, the parity of 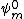 determines the parity of the entire integrand; if it is odd, the integrand is odd, and the integral is zero. With 0 representing the ground state, odd values (i.e. m, n = 1, 3, 5, ...) produce odd wave functions, making the coefficients zero. This is answer choice (B). determines the parity of the entire integrand; if it is odd, the integrand is odd, and the integral is zero. With 0 representing the ground state, odd values (i.e. m, n = 1, 3, 5, ...) produce odd wave functions, making the coefficients zero. This is answer choice (B).
94709
2007-10-14 21:49:38 |
I agree it's evil in the sense they used n=0 for the ground state,,,
Two fundamental knowledges...Q.M. and Perturbation.
Very fundamental knowledge about QM; inifinite solution form a complete basis set to span hilbert space.
Perturbation is not only in quantum mechanics, but everywhere else in general. Better be fresh...
1. Sudden approximation tells that all even functions about the origine is likely to be gone.
2. Using odd functions in original summation, one must be able to complete the basis set since there are infinite many.
3. Since the original potential is an infinite well, the ground state is, of course, even. So 1st excited states, 3rd, 5th, will remain.
Only 3 steps in head, and no calculation but fundamental knowledge about Q.M. Easier than those problems that require memorization of equations.
|
Jeremy
2007-10-20 12:26:48 |
94709,
There are a couple things you say that I disagree with:
1. "Even functions... likely to be gone." It's just the opposite actually. Answer choice (B) says the new ground state is a sum of even functions - remember, odd n corresponds to odd unperturbed wave functions.
2. "Using odd functions in original summation, one must be able to complete the basis set since there are infinite many." Not true. For example, you can't write an even function as a sum of odd functions (the sum of odd functions is an odd function).
|
94709
2007-10-21 21:06:18 |
Jeremy,
Thank you for your reply.
About the first correction:
Given that the potential is infinite-well, I think the ground state is an even function with one node at the origin. New potential is an even function which surpress all even functions. Defining the ground state with n=0, all even n terms express even functions. Hence, odd n remains, meaning that odd functions remain. This is an argument of "Is the wavefunction of the ground state in infinite potential well even or odd function?" With one node at the center, x=0, the ground state is even. Hence, even n express even functions, and odd n expresse odd functions.
About the second correction:
I am sorry that I did not explicitly mention my assumption in every step. As a consequence from previous steps, what I mean by "function can be spanned by odd terms" is that odd functions can be spanned by odd terms. I stupidly assumed this is very clear, and did not mention at this stage.
Thanks for your comment.
|
|  | freeform
2006-11-30 18:29:07 | Rather than a square well, the potential is a well with a dent in the center so that it slightly looks like a W. Only eigenfunctions with nodes at center of well will be admitted---there are the 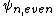 . .
Jeremy
2007-10-10 12:39:59 |
freeform, you made the same mistake I did. Because the counting starts at 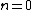 , even , even  corresponds to even wave functions. The new ground state does NOT have a node at the center of the well as it is an even function. corresponds to even wave functions. The new ground state does NOT have a node at the center of the well as it is an even function.
|
|  | dirichlet
2006-11-21 11:27:46 | I think all the even term will go out because the even functions are of odd parity in this case.
|  | dirichlet
2006-11-21 11:22:42 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
