|
GR8677 #22 |
|
|
Problem
|
|
 |
Electromagnetism }Lorentz Transformation
When an electric field is Lorentz-transformed, afterwards, there might be both a magnetic and electric field (in transverse components). Or, more rigorously, one has,
\\
E_z'&=& \gamma(E_z+vB_y)\\
B_x' &=& B_x\\
B_y' &=& \gamma(B_y + E_z v/c^2)\\
B_z' &=& \gamma(B_z-vE_y/c^2),<br />
\end{eqnarray})
for motion in the  direction.
(A) Obviously not. Suppose initially, one has just 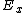 , afterwards, there's still  .
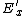(B) True, as can be seen from the equations above.
(C) Not true in general. Suppose 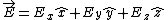 . Afterwards, the transverse components are off by a  even if there's no B field to start with.
(D) Nope.
(E) Mmmm... no need for gauge transformations.
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
FortranMan
2008-10-17 23:15:56 | For more on this topic, look around for Relativistic Electrodynamics, specifically in Griffiths section 12.3. Imagine the case of a large parallel-plate capacitor moving perpendicular to their surface areas, and imagine what the Lorentz contraction does to the charge distributions on the plates. This ends up increasing the electric field that's perpendicular to the direction of motion. Note for a parallel-plate capacitor situated such their motion is parallel to their surfaces, this contraction does not occur and the field remains unchanged. |  | grae313
2007-10-07 15:50:57 | On choice (E), does the Lorentz transformation already assume the Lorentz guage?
rorytheherb
2008-10-06 10:22:16 |
yeah I'm looking at griffiths EM and it's not really illuminating this particular question. i knew of course that E and B mix in S.T.R., but when I saw choice E, I recalled the Lorentz gauge and got duped. Can anyone clarify why how we can say E and B mix _without_ first specifying a gauge?
|
dean
2008-10-09 21:00:55 |
I'm not sure there's any relevance at all. Gauge transformations talk about potentials, not fields. A (the vector potential) may change depending on what gauge you're using, but B does not, and can not, else we'd have a physically different situation. Lorentz transformations talk about fields directly in different inertial frames.
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
|
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
