|
|
|
| All Solutions of Type: Thermodynamics | | 0 | Click here to jump to the problem! | GR8677 #14
|
Thermodynamics }Exact differentials }Exact differentials
The key equation is:  , and its players, , and its players, 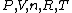 , are terms one should be able to guess. , are terms one should be able to guess.
(A) True, according to the ideal gas law. (This is also the final step in deriving Mayer's Equation, as shown below.)
(B) This translates into the statement 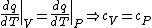 .The problem gives away the fact that for an ideal gas .The problem gives away the fact that for an ideal gas 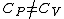 . B can't be right. . B can't be right.
(C) According to the ideal gas law, the volume might change.
(D) False. An ideal gas's internal energy is dependent only on temperature. More elegantly, 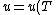) . .
(E) Heat needed for what?
If one is interested in the formal proof of the relation 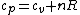 , read on about Mayer's equation: , read on about Mayer's equation:
For thermo, in general, there's an old slacker's pride line that goes like, ``When in doubt, write a bunch of equations of states and mindlessly begin taking exact differentials. Without exerting much brainpower, one will quickly arrive at a brilliant result." Doing this,
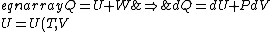&\Rightarrow& dU=\left.\partial_T U\right|_T +\left.\partial_V U\right|_V\\
PV=nRT&\Rightarrow&PdV+VdP=nRdT<br />
\end{eqnarray})
Plugging in the first law of thermodynamics into the 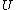 equation of state, one gets equation of state, one gets 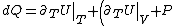dV=\left.\partial_T U\right|_T+PdV) , where the last simplification is made by remembering the fact that the internal energy of an ideal gas depends only on temperature. , where the last simplification is made by remembering the fact that the internal energy of an ideal gas depends only on temperature.
(Taking the derivative with respect to T at constant volume, one gets 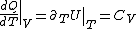 .) .)
Plugging in the simplified result for  into the third equation of state, the ideal gas equation, one gets: into the third equation of state, the ideal gas equation, one gets: 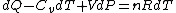 . Taking the derivative at constant pressure, one gets: . Taking the derivative at constant pressure, one gets:
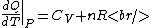
So, one sees that it is the ideal gas equation that makes the final difference. The work of an ideal gas changes when temperature is varied.
|
| 5 | Click here to jump to the problem! | GR8677 #15
|
Thermodynamics }Phase Diagram }Phase Diagram
Recall that for an ideal gas 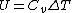 and and  . Don't forget the first law of thermodynamics, . Don't forget the first law of thermodynamics, 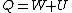 . .
For 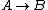 , , 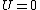 , since the temperature is constant. Thus, , since the temperature is constant. Thus, 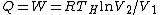 . .
For 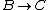 , , 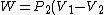=R(T_c-T_h)) . . 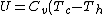) , and thus , and thus 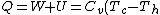-R(T_h-T_c)) . .
For 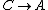 , , 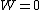 , , 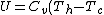) , thus , thus 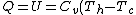) . .
Add up all the Q's from above, cancel the 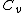 term, to get term, to get -R(T_h-T_c)) , as in choice (E).s , as in choice (E).s
|
| 6 | Click here to jump to the problem! | GR8677 #16
|
Thermodynamics }Mean Free Path }Mean Free Path
Air is obviously less dense than the atomic radius 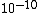 , thus choices (C), (D), and (E) are out. Air is not dilute enough that the distance between particles is actually within human visible range, as in (A)! Thus, the answer must be (B). (Note how this problem exemplifies the usefulness of common sense.) , thus choices (C), (D), and (E) are out. Air is not dilute enough that the distance between particles is actually within human visible range, as in (A)! Thus, the answer must be (B). (Note how this problem exemplifies the usefulness of common sense.)
|
| 10 | Click here to jump to the problem! | GR8677 #91
|
Thermodynamics }Second Law }Second Law
The Second Law of thermodynamics has to do with entropy; that entropy can never decrease in the universe. One form of it states that from hot to cold things flow. A cooler body can thus never heat a hotter body. Since the oven is at a much lower temperature than the wanted sample temperature, the oven can only heat the sample to a maximum of 600K without violating the Second Law.
(This solution is due to David Latchman.)
(Also, since the exam is presumably written by theorists, one can narrow down the choices to either (D) or (E), since the typical theorist's stereotype of experimenters usually involves experimenters attempting to violate existing laws of physics---usually due to naivity.)
|
| 11 | Click here to jump to the problem! | GR8677 #5
|
Thermodynamics }Degree of Freedom }Degree of Freedom
Acording to the Equipartition Theorem, there is a $kt/2$ contribution to the energy from each degree of quadratic freedom in the Hamiltonian. In equation form, the average total energy is 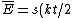) , where s is the degrees of freedom. , where s is the degrees of freedom.
For a n-dimensional 1-particle system, the Hamiltonian is 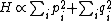 , where , where 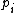 ( (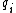 ) refer, respectively, to the ) refer, respectively, to the 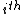 component of momentum (position). component of momentum (position).
Thus, for a 3-dimensional 1-particle system, one has 6 quadratic terms in the Hamiltonian, as in  . .
Plugging in s=6, one finds that the average energy is 3kT.
(This revised solution is due to the GREPhysics.NET user kolndom.)
|
| 16 | Click here to jump to the problem! | GR8677 #48
|
Thermodynamics }RMS Speed }RMS Speed
In case one forgets the RMS speed, one does not need to go through the formalism of deriving it with the Maxwell-Boltzmann distribution. Instead, one can approximate its dependence on mass and temperature by 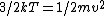 . One thus has . One thus has 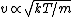 . For the ratio of velocities, one has . For the ratio of velocities, one has 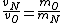 . Plug in the given molecular masses for Oxygen and Nitrogen to get choice (C). . Plug in the given molecular masses for Oxygen and Nitrogen to get choice (C).
Incidentally, the trick for memorizing the diatomic gasses is Have No Fear Of Ice Cold Beer (Hydrogen, Nitrogen, Florine, Oxygen, Iodine, Chlorine, Bromine).
|
| 17 | Click here to jump to the problem! | GR8677 #16
|
Thermodynamics }Carnot Engine }Carnot Engine
Recall the common-sense definition of the efficiency  of an engine, of an engine,
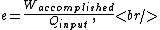
where one can deduce from the requirements of a Carnot process (i.e., two adiabats and two isotherms), that it simplifies to
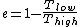
for Carnot engines, i.e., engines of maximum possible efficiency. (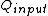 is heat put into the system to get stuff going, is heat put into the system to get stuff going, 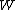 is work done by the system and is work done by the system and 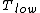 ( ( ) is the isotherm of the Carnot cycle at lower (higher) temperature.) ) is the isotherm of the Carnot cycle at lower (higher) temperature.)
The efficiency of the Carnot engine is thus 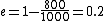 , where one needs to convert the given temperatures to Kelvin units. (As a general rule, most engines have efficiencies lower than this.) The heat input in the system is , where one needs to convert the given temperatures to Kelvin units. (As a general rule, most engines have efficiencies lower than this.) The heat input in the system is 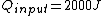 , and thus , and thus 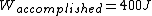 , as in choice (A). , as in choice (A).
|
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
