|
GR9277 #16
|
|
|
Problem
|
|
\prob{16}
An engine absorbs heat at a temperature of 727 degrees Celsius and exhausts heat at a temperature of 527 degrees Celsius. If the engine operates at a maximum possible efficiency, for 2000 joules of heat input the amount of work the engine performs is most nearly
- 400 J
- 1450 J
- 1600 J
- 2000 J
- 2760 J
|
Thermodynamics }Carnot Engine }Carnot Engine
Recall the common-sense definition of the efficiency  of an engine, of an engine,
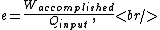
where one can deduce from the requirements of a Carnot process (i.e., two adiabats and two isotherms), that it simplifies to
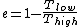
for Carnot engines, i.e., engines of maximum possible efficiency. (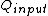 is heat put into the system to get stuff going, is heat put into the system to get stuff going, 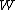 is work done by the system and is work done by the system and 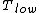 ( (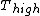 ) is the isotherm of the Carnot cycle at lower (higher) temperature.) ) is the isotherm of the Carnot cycle at lower (higher) temperature.)
The efficiency of the Carnot engine is thus 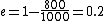 , where one needs to convert the given temperatures to Kelvin units. (As a general rule, most engines have efficiencies lower than this.) The heat input in the system is , where one needs to convert the given temperatures to Kelvin units. (As a general rule, most engines have efficiencies lower than this.) The heat input in the system is 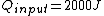 , and thus , and thus 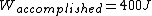 , as in choice (A). , as in choice (A).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
hooverbm
2012-10-05 08:58:41 | I think you can get around not even calculating efficiency.
We know that the relationship between Qs and Ts:
Qc/Qh = Tc/Th (h = hot, c = cold)
The work:
W = Qh-Qc
Solve for Qc above, and plug into work. You get an answer for Qc ~ 1400,
So W ~ 600J, which is closest to 400J.
Thus A |  | heypete
2010-11-05 14:56:52 | Where, exactly, did the values 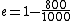 come from when explaining the Carnot efficiency? Those values are not found anywhere in the problem. Is that a typo? come from when explaining the Carnot efficiency? Those values are not found anywhere in the problem. Is that a typo?
When I solve for e, I find 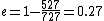 , so , so 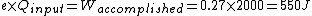
Certainly, 550 J is closer to 400 J (choice A) than any other value, but it still seems a bit rough. Am I doing something incorrectly, or is there an error in the posted solution?
z3phx
2010-11-06 19:53:20 |
The temperatures are in Kelvin
|
neon37
2010-11-10 11:22:00 |
yep all temperatures in Kelvin should be used for all thermo calculations in SI units. The numbers were suspiciously odd which made me realize this.
|
aziza
2013-09-30 18:27:41 |
i dont think you have to convert to kelvin. Tc/Th is a ratio...the units cancel out
|
justin_l
2013-10-15 11:29:55 |
okay, that's just silly. it's an affine transformation, so ratios aren't perserved.rnrncounterexample: 2 C / 1 C vs 279 K / 274 K.rnrnThe celsius ratio is 2, the kelvin ratio is very nearly 1.
|
|  | mm
2007-09-19 02:47:04 | Remenbering Q_1 / T_1 + Q_2 / T_2 = 0, you can get the answer easily.
petr1243
2008-01-15 20:24:45 |
Since entropy is a state function, the net change in entropy must be zero for one complete cycle(this could be sought out, when one plots T as a function of S. So you should have a difference of the the high and low entropies, instead of a sum.
|
gt2009
2009-06-14 20:12:52 |
One of the Q's is implicitly negative. It would be a difference if you put absolute values around each Q.
|
Sagan_Man
2012-02-02 17:38:55 |
Wait, but this gives 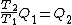 , which is , which is 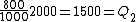 ...which is wrong? ...which is wrong?
|
morenogabr
2012-10-06 12:08:55 |
should be
Q_1=Q_2)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
