|
GR9277 #15
|
|
|
Problem
|
|
\prob{15}
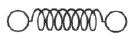
The classical model of a diatomic molecule is a springy dumbbell, as shown above, where the dumbbell is free to rotate about axes perpendicular to the spring. In the limit of high temperature, what is the specific heat per mole at constant volume?
- 3R/2
- 5R/2
- 7R/2
- 9R/2
- 11R/2
|
Statistical Mechanics }Heat Capacity }Heat Capacity
Note that this problem wants the regime of high temperatures, and thus the answer is not 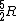 from classical thermodynamics, but rather from classical thermodynamics, but rather 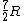 . .
The problem suggests that a quantized linear oscillator is used. From the energy relation \hbar \nu) , one can write a partition function and do the usual Stat Mech jig. Since one is probably too lazy to calculate entropy, one can find the specific heat (at constant volume) from , one can write a partition function and do the usual Stat Mech jig. Since one is probably too lazy to calculate entropy, one can find the specific heat (at constant volume) from 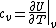 , where , where _V) , where , where 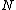 is the number of particles, is the number of particles, 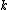 is the Boltzmann constant. is the Boltzmann constant.
There are actually three contributions to the specific heat at constant volume. 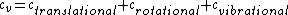 . Chunk out the math and take the limit of high temperature to find that . Chunk out the math and take the limit of high temperature to find that  . .
|
|
|
Alternate Solutions |
sharpstones
2006-08-26 13:26:14 | There is a much simpler way:
Cv = Ctrans + Crotational + Cvibrational
Each quadratic degrees of freedom (QDF) contributes (1/2)R to Cv
QDF trans = 3
QDF rot = 2
QDF vib = 2
=> 3+2+2 = 7
7*(1/2)R = (7/2)R => the answer
The trick is with the vibrational modes:
Vibrational => *IMPORTANT PART* Each vibrational mode is 2 degrees of freedom, one for the Kinetic Energy and one for the Potential. A Diatomic molecule only has 1 vibrational mode, hence 2 vibrational degrees of freedom.
Trans => 3 degrees of freedom because 3 dimensions to translate
Rotational => There are 3 possible rotation directions in 3d but the degree of freedom running down the length of the diatomic molecule doesn't count (makes sense if you think about it since it is symmetric around that axis). Thus there are 2 degrees of rot freedom in a diatomic
kevglynn
2006-10-04 16:20:40 |
You never mention high temperatures in this solution, which makes me think it may be oversimplified and/or wrong. Not to be a pain, just wondering.
|
herrphysik
2006-10-08 23:59:57 |
kevglynn: In the limit of high temperature in this problem just means that the rotational and vibrational degrees of freedom are active.
|
|  |
|
|
Comments |
francesco
2017-09-13 19:46:01 | May \"high temperature\" is another confusing ETS redundant info?\r\n\r\nSimply looking at the classical item, if a rigid dumbbell has 5 d.o.f. (3 for each end - 1 for the rigid binding), a springy one would add 2 further d.o.f. (1 kinetic + 1 potential) so the equipartition of energy would give U = 7/2RT and C = 7/2R |  | greatspirits
2012-10-30 15:39:51 | It's been a small while since I thought about this type of problem. I agree with the number of degrees of freedom appoach divided by 2 . As to the determination of degrees of freedom method posted by sharpstones, I am not on the same page. There are three translational degrees of freedom for the kinetic energy of each atom, total=6. Rotational energy considerations are irrellevant now because the rotational dynamics of the atom are already determined by the translational dynamics of each atom, no additional energy here. This leaves the potential energy of the spring=just 1 degree of freedom, not 2. total=7 So, Cv=7/2R.
djh101
2014-08-29 14:03:07 |
I suppose it's a little late to be responding for the author's benefit, but in case anyone else is reading this:
Translation is translation of the whole system, so three degrees of freedom for translation in three dimensions. Because the molecule is linear, rotation only has two degrees of freedom, perpendicular to the axis of the molecule.
|
|  | greatspirits
2012-10-30 15:38:07 | It's been a small while since I thought about this type of problem. I agree with the number of degrees of freedom appoach divided by 2 . As to the determination of degrees of freedom method posted by sharpstones, I am not on the same page. There are three translational degrees of freedom for the kinetic energy of each atom, total=6. Rotational energy considerations are irrellevant now because the rotational dynamics of the atom are already determined by the translational dynamics of each atom, no additional energy here. This leaves the potential energy of the spring=just 1 degree of freedom, not 2. total=7 So, Cv=7/2R. |  | greatspirits
2012-10-30 15:32:36 | It's been a small while since I thought about this type of problem. I agree with the number of degrees of freedom appoach divided by 2 . As to the determination of degrees of freedom method posted by sharpstones, I am not on the same page. There are three translational degrees of freedom for the kinetic energy of each atom, total=6. Rotational energy considerations are irrellevant now because the rotational dynamics of the atom are already determined by the translational dynamics of each atom, no additional energy here. This leaves the potential energy of the spring=just 1 degree of freedom, not 2. total=7 So, Cv=7/2R. |  | tederoony
2011-11-09 17:59:50 | This problem is on crack. There is only 1 vibrational degree of freedom. The right answer is 3R. rnrnSee wikipedia: http://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)#Example:_diatomic_gasrn |  | so1oeclipse
2010-10-17 15:55:59 | What would the alternative be... say, if they ask for 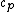 . .
ticklecricket
2010-11-11 13:37:45 |
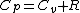
|
|  | skyer7
2007-10-08 01:42:11 | Sorry, It is the Law of Energy Equi-partition and the Kinetic Energy part is 3RT. |  | skyer7
2007-10-08 01:41:09 | Sorry, It is the Law of Energy Equi-partition and the Kinetic Energy part is 3R. |  | skyer7
2007-10-08 01:39:00 | Sorry, It is the Law of Energy Equi-partition and the Kinetic Energy part is 3R/2. |  | skyer7
2007-10-08 01:28:42 | Sorry, It is the Law of Energy Equi-partition and the Kinetic Energy part is 3R/2. |  | sharpstones
2006-08-26 13:26:14 | There is a much simpler way:
Cv = Ctrans + Crotational + Cvibrational
Each quadratic degrees of freedom (QDF) contributes (1/2)R to Cv
QDF trans = 3
QDF rot = 2
QDF vib = 2
=> 3+2+2 = 7
7*(1/2)R = (7/2)R => the answer
The trick is with the vibrational modes:
Vibrational => *IMPORTANT PART* Each vibrational mode is 2 degrees of freedom, one for the Kinetic Energy and one for the Potential. A Diatomic molecule only has 1 vibrational mode, hence 2 vibrational degrees of freedom.
Trans => 3 degrees of freedom because 3 dimensions to translate
Rotational => There are 3 possible rotation directions in 3d but the degree of freedom running down the length of the diatomic molecule doesn't count (makes sense if you think about it since it is symmetric around that axis). Thus there are 2 degrees of rot freedom in a diatomic
kevglynn
2006-10-04 16:20:40 |
You never mention high temperatures in this solution, which makes me think it may be oversimplified and/or wrong. Not to be a pain, just wondering.
|
herrphysik
2006-10-08 23:59:57 |
kevglynn: In the limit of high temperature in this problem just means that the rotational and vibrational degrees of freedom are active.
|
skyer7
2007-10-08 01:24:38 |
I agree with sharpstones and herrphysik. To me, it seems pretty straightforward to use the Law of Equi-partition. What's more, there is no suggestion in this problem that "a quantized linear oscillator is used" as the official solution states. And certainly the classical thermodynamics gives the right answer 7R/2 right away. It is the Kinetic Energy part that is 5RT/2.
|
tau1777
2008-11-02 15:21:11 |
hi, i tried to use this solution when i was solving it but i didn't get two vibrational degrees of freedom. i was just thinking about the compression of the spring. does the stretching also count as one. can anyone please just explain this some more.
|
apr2010
2010-04-08 15:57:15 |
There is a question in one of the other test asking the same. For low temperatures it would have only 3/2 degrees (3 translational) is stated in it's problem text.
|
gravity
2010-11-07 23:27:06 |
For more info on this, go to the bottom of this page: http://hyperphysics.phy-astr.gsu.edu/hbase/Kinetic/shegas.html
|
neon37
2010-11-10 11:02:47 |
Yes high temperature means the especially the vibrational modes are active. At colder temperatures, the vibrational modes disappear and the model is more like a solid dumbbell rather than a springy one.
|
Almno10
2010-11-12 12:32:30 |
High temperature is precisely when the equipartition theorem applies. This is correct.
(At low T, some degrees of freedom are said to be "frozen out," so the actual mean energy is less than equipartition predicts.)
|
aam
2014-04-01 17:40:57 |
This is correct.
"Each rotational and translational degree of freedom will contribute R/2 in the total molar heat capacity of the gas. Each vibrational mode will contribute R to the total molar heat capacity, however. This is because for each vibrational mode, there is a potential and kinetic energy component. Both the potential and kinetic components will contribute R/2 to the total molar heat capacity of the gas. Therefore, a diatomic molecule would be expected to have a molar constant-volume heat capacity of"
See "Diatomic Gas" in this wikipedia article:
http://en.wikipedia.org/wiki/Heat_capacity
|
PGREwannabeMaster
2014-07-21 14:34:57 |
For rotational how can there ever be 3 rotation directions? In 3D wouldn't it be just theta and phi?
|
wgjohnson
2014-08-28 12:32:06 |
sharpstones is right--at high temperature where vibrational degree of freedom is truly activated,
Cv = 7/2R (ideal non-interacting dumb-bells). See D Schroeder text, plot of heat capacity of molecular hydrogen
|
djh101
2014-08-29 14:16:59 |
Theta and phi are the coordinates of an object in spherical coordinates, used to indicate position. Rotational degrees of freedom are the ability to rotate about each coordinate axis.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
