|
GR9677 #13
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
benjamin_DW
2016-10-27 14:18:09 | What\'s not clear to me is why the substance **must** cool at the same rate that we heated it. Just because we heated it at a rate of 100W does not mean it will necessarily cool at a rate of 100W. In fact, by Newton\'s law of cooling, the temperature ) is given by: \r\n\r\n is given by: \r\n\r\n) \r\n\r\nWhere \r\n\r\nWhere ) is the background temperature, and is the background temperature, and 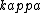 is a constant dependent on the geometry of the material.[and even this of course, is an approximation] is a constant dependent on the geometry of the material.[and even this of course, is an approximation]
rweads
2017-04-30 01:28:20 |
since the liquid does not boil, and the heat element has been in the water for a long time, the system must be in thermal equilibrium where the rate of heat added is equal to the rate that heat is dissipated. It is then very reasonable that for small deviations from that equilibrium temperature the rate of heat loss will be the same.
|
yummyhat
2017-10-27 22:44:30 |
thanks rweads (and einstein)
|
|  | cczako
2013-10-17 17:07:38 | The easiest way to do this is to use units. 4200 J/ kg C times 1 C and 1 kg (1L=1kg) is 4200 J. Watts is Joules per second so divide 4200 J by 100 J/s and you get 42 s. |  | asafparis
2009-04-02 13:10:33 | 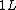 of water is not of water is not 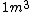
shak
2010-08-14 09:51:27 |
1 L of water is exactly one cubic meter!
m= v*r
|
BerkeleyEric
2010-09-21 19:13:11 |
1 liter is equal to 0.001 cubic meters, which does correspond to 1 kg for water
|
Rtrt
2015-10-13 08:49:28 |
yes . 1L is 1 kg but it is not 1m^3. density of water is 1000 kg/m^3. 1 L is 0.001 m^3. So mass is 1 kg.
|
|  | naama99
2006-11-21 08:18:36 | Since the formula for specific heat c has delta T in it, why do you take 1 degree as delta T instead of 99?
welshmj
2007-07-31 14:37:33 |
because the problem says that it cools by 1 degree not that it cools TO 1 degree which means that the change in temperature (delta T) is 1 degree not 99 degrees.
|
|  | vortex
2005-12-04 16:09:10 | 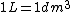 not not 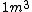 ,and an arrow would be better before 1 kg. ,and an arrow would be better before 1 kg. |  | yosun
2005-11-10 23:32:23 | angiep: the specific heat of water is 4200 J/kg and not 2200. thanks for the typo-alert. |  | angiep
2005-11-10 23:14:50 | I dont feel like this problem makes any sense at all. It is worded completely wrong.
einstein
2006-03-31 02:32:57 |
In fact it is worded perfectly correctly. The statement that the 100-Watt heating element remains for a long time but the water does not boil informs us that the water must be disipating the energy at precisely this rate. Hence P_{out} =100W
|
Imperate
2008-09-04 09:02:50 |
I can see it makes sense now thanks to einstein's comment. However I have to agree that this question is worded very badly. The sentance "the heating element is on for a long time and the water although close to boiling does not boil" makes it sound like the water heats up to being close to boiling, not that the water started close to being at boiling point and despite the heaters presence,did not boil.rnWould have been much better to say the temperature of the water remains static, despite heater of 100W being placed in it.
|
tachyon788
2009-10-06 09:58:33 |
I agree with Imperate. I thought the question meant that the heater heated the water (and increased the temperature) until it was removed right before the water started to boil. In that case, the whole heater thing seemed like a red herring. With only 1.7 minutes per question, we don't really have time to decipher poorly worded questions...
|
hdcase
2009-11-01 22:06:40 |
I disagree with Imperiate. The question isn't saying that the water started at close to boiling - rather, it is saying that the steady state of the system is such that at the steady state temperature (which is close to 100 C) the system is losing 100 W. I think it is worded in such a way that one can glean that information without it having to be stated directly.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
