socolenco_
2015-09-18 23:21:35 | You have [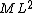 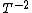 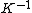 ] for entropy and [ ] for entropy and [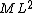 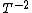 ] for internal energy and their ratio is ] for internal energy and their ratio is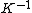 , which is exactly the reciprocal of the Kelvin temperature T°.\r\n , which is exactly the reciprocal of the Kelvin temperature T°.\r\n |  |
ryanjsfx
2014-09-21 13:08:27 | I'm not sure my logic is sound but I got this just by process of elimination.
We're looking for inverse of T, so eliminate A and B since they look normal (not inverted) expressions.
If T changes, so does U [U = U(T)]. Eliminate C and D.
That leaves E. |  |
spacemanERAU
2009-10-18 18:22:02 | how do you know the volume is constant?
neon37
2010-11-03 11:30:43 |
because 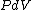 needs to be zero in needs to be zero in 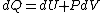 So that we can use So that we can use 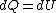 . Otherwise, the answer would be complicated and you would have to reciprocate the whole thing. And there is no complicated answer in the question. . Otherwise, the answer would be complicated and you would have to reciprocate the whole thing. And there is no complicated answer in the question.
|
flyboy621
2010-11-14 22:13:36 |
You don't know the volume is constant. What you know is that IF you hold the volume constant while differentiating the entropy with respect to internal energy, you get the inverse of the temperature. Whenever you take a partial derivative, you have to hold something constant.
|
|  |
Hardik
2008-11-06 13:11:39 | Use statistical definition of temperature and entropyrnrnvoila |  |
student2008
2008-10-12 06:31:38 | Actually, one can recall the general differential expression for the energy of a system 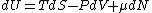 . Thus, . Thus, 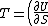_{N,V}) . .
flyboy621
2010-11-14 22:14:45 |
Perfect solution!
|
|  |
carlospardo
2007-10-03 13:10:49 | All this is unnecessary. When obvious, select the answer with correct units.
djh101
2014-08-28 13:46:39 |
I can recall dU = TdS - PDV off the top of my head better than units of entropy (which I would probably derive from that equation anyway).
|
|  |
carlospardo
2007-10-03 13:10:48 | All this is unnecessary. When obvious, select the answer with correct units. |  |
WTarrasque
2006-11-03 19:12:23 | In the compiled solutions PDF, the reciprocal is only taken of one side. Thus it has:
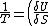 _V ) instead of instead of 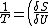 _V ) |  |
jax
2005-12-03 10:59:32 | You mean _V) is the correct answer, right? is the correct answer, right?
yosun
2005-12-04 23:11:43 |
right. note that the above is given in terms of inverse Temperature --- a commonly used multiplier quantity in thermo.
|
jax
2005-12-05 06:51:18 |
Doesn't the question ask for inverse temperature? When I worked it out I got 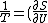_V)
|
walczyk
2011-03-10 21:54:37 |
at extremely low energies, a small change in energy amounts to a huge gain in entropy, so the inverse T is huge, and T is tiny.
|
|  |
